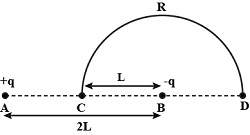
From figure, \(A C=L, B C=L, B D=B C=L\)
\(A D=A B+B D=2 L+L=3 L\)
Potential at \(C\) is given by
\(V_{C}=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{A C}+\frac{(-q)}{B C}\right]=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{L}-\frac{q}{L}\right]=0\)
Potential at \(D\) is given by
\(V_{D} =\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{A D}+\frac{(-q)}{B D}\right]=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q}{3 L}-\frac{q}{L}\right]\)
\(=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{L}\left[\frac{1}{3}-1\right]=\frac{-q}{6 \pi \varepsilon_{0}}\)
Work done in moving charge \(+Q\) along the semicircle \(CRD\) is given by
\(W=\left[V_{D}-V_{C}\right](+Q)=\left[\frac{-q}{6 \pi \varepsilon_{0}}-0\right](Q)=\frac{-q Q}{6 \pi \varepsilon_{0} L}\)
Comments : Potential at \(C\) is zero because the charges are equal and opposite and the distances are the same. Potential at \(D\) due to \(-q\) is greater than that at \(A\) \((+q),\) because \(D\) is closer to \(B .\) Therefore it is negative.
Download our appand get started for free
Similar Questions
- 1બિંદુ $ (x,y,z) $ (મીટરમાં) આગળનું વિદ્યુતસ્થિતિમાન $ V=4x^2$ $volt$ છે. બિંદુ $(1,0,2)$ આગળ વિદ્યુતક્ષેત્રની તીવ્રતા $(V/m$ માં) ......View Solution
- 2View Solutionકેપેસિટન્સનું પરિમાણિક સૂત્ર શું થાય?
- 3$1.5 \mu \mathrm{F}$ સંધારકતા ધરાવતા કેપેસીટર (સંધારક)ની પ્લેટ વચ્ચેનું વિદ્યુતક્ષેત્ર, જ્યારે પ્લેટને પાતળા તારથી જોડવવામાં આવે છે ત્યારે $6.6 \mu \mathrm{s}$ માં તેના પ્રારંભિક મૂલ્ય કરતાં ધરીને એક તૃતિયાંશ થાય છે. આ તારનો અવરોધ. . . . . . .$\Omega$ છે. $(\log 3=1.1$ આપેલ છે.)View Solution
- 4સમાંતર પ્લેટ કેપેસીટરની પ્લેટો $100\ V$ સુધી વિદ્યુતભારીત કરેલ છે. હવે $2\ mm$ જાડાઇની પ્લેટને બે પ્લેટો વચ્ચે દાખલ કરવામાં આવે છે તથા સમાન વિદ્યુત સ્થીતીમાન જાળવી રાખવા માટે કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર $1.6\, mm $ વધારવામાં આવે તો પ્લેટનો ડાઇ ઇલેકટ્રીક અચળાંક....View Solution
- 5બે $6\ pF$ વાળા કેપેસીટરોને શ્રેણીમાં જોડી જોડાણને સમાંતર $5000\, V$ આપવામાં આવે છે. હવે જોડાણને તોડીને તેમને સમાંતરમાં જોડવામાં આવે તો પ્લેટો વચ્ચેનું વિદ્યુતસ્થીતીમાન....View Solution
- 6કોઈ ક્ષેત્રમાં વિદ્યુતસ્થિતિમાન $V(x) = 4x^2\,volts$ મુજબ પ્રવર્તે છે.$1\,m$ બાજુ ધરાવતા ઘનના કેન્દ્ર પર કેટલો વિજભાર (કુલંબમાં) હશે?View Solution
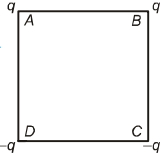
- 7આકૃતિમાં દર્શાવ્યા મુજબ ચોરસનાં શિરોબિંદુઓ પર વિદ્યુતભાર મૂકેલા છે.આ ચોરસના કેન્દ્ર પર વિદ્યુતક્ષેત્ર $\vec E$ અને વિદ્યુતસ્થિતિમાન $V$ છે.જો $A$ અને $B$ પરના વિદ્યુતભારને $D$ અને $C$ સ્થાને રહેલા વિદ્યુતભાર સાથે અદલા-બદલી કરવામાં આવે, તો ચોરસના કેન્દ્ર પર .......View Solution
- 8એક કણ $A$ અનો વિદ્યુતભાર $+q$ અને $B$ નો વિદ્યુતભાર $+9\ q$ છે. પ્રત્યેક કણનું દળ $m$ સમાન છે. જો બંને કણોને સ્થિર સ્થિતિએથી સમાન સ્થિતિમાન તફાવત સાથે છોડવામાં આવે તો તેઓની ઝડપનો ગુણોત્તર ....... હશે.View Solution
- 9બે એકસરખી રચના અને ક્ષમતાવાળા કેપેસીટરોને $V$ જેટલા સ્થિતિમાન તફાવતે સમાંતરે રાખેલ છે. જ્યારે તે બંને પુરેપુરા ચાર્જ થઈ જાય ત્યારે એકની ધન પ્લેટને બીજાની ઋણ પ્લેટ સાથે અને બીજાની દળ પ્લેટ સાથે ઋણ પ્લેટને જોડી દેવામાં આવે તો આમાં થતો ઉર્જાનો વ્યય શોધો.View Solution
- 10$50\, \mu F$ ધરાવતા કેપેસિટરને $100\, V$ ચાર્જ કરેલ છે.બેટરી દૂર કરીને બે પ્લેટ વચ્ચેનું અંતર બમણું કરવા માટે કેટલું કાર્ય કરવું પડે?View Solution
