બે બિંદુવત વિદ્યુતભારો $+ 9\ e$ અને $+e$ એકબીજાથી $16\, cm$ દૂર મૂકેલા છે. તેમની વચ્ચે ત્રીજો વિદ્યુતભાર $q$ ને ક્યાં મૂકવામાં આવે કે જેથી તે સંતુલન સ્થિતિમાં હોય.
Medium
b
Let the charge \(q\) is placed at a distance \(x\) from \(+9 e\) and inbetween charges \(+9 e\) and te
Let the charge \(q\) is placed at a distance \(x\) from \(+9 e\) and inbetween charges \(+9 e\) and te
Using Coulomb's law,
\(\frac{K \cdot 9 e \cdot q}{x^2}=\frac{K \cdot q \cdot e}{(16-x)^2}\left\{F=\frac{K q_1 q_2}{r^2}\right\}\)
\(\left(\frac{16-x^2}{x}\right)^2=\frac{1}{9}\)
\(\frac{16}{x}-1=\pm \frac{1}{3}\)
\(\Rightarrow \frac{16}{x}=\frac{4}{3} \text { or } \frac{2}{3}\)
\(\Rightarrow x=\frac{3 \times 16}{4} \text { or } \frac{3 \times 16}{2}\)
\(\therefore x=12\,cm \text { or } 24\,cm\)
As the charge \(q\), can be equilibrium present only when its is kept inbetween charges \(+9 e\) and \(+e\), correct answer is \(x=12\,cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉગમબિંદુ $(0,0,0)$ આગળ રહેલ એક વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $\overrightarrow{\mathrm{p}}=(-\hat{\mathrm{i}}-3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}) \times 10^{-29}\; \mathrm{C} \cdot \mathrm{m}$ છે.ડાયપોલને કારણે $\overrightarrow{\mathrm{r}}=+\hat{\mathrm{i}}+3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$ આગળ રહેલ વિદ્યુતક્ષેત્ર કોને સમાંતર હોય? ($\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{p}}=0)$View Solution
- 2બે સમાન દળ $m$ અને વિરુદ્ધ વિજભાર $q$ ને $d$ અંતરે મૂકીને ડાયપોલ બનાવવામાં આવે છે.જેને એકસમાન વિદ્યુતક્ષેત્ર $E$ માં મુકેલ છે.જો તેને સંતુલન અવસ્થામાથી થોડુક ભ્રમણ કરવવામાં આવે તો તેની કોણીય આવૃતિ $\omega $ કેટલી થશે?View Solution
- 3એક વિસ્તારમાં વિદ્યુતક્ષેત્ર ત્રિજ્યાકીય રીતે બહારની તરફ છે. અને કોઈ બિંદુ પાસે તે $E=250 r \,V / m$ છે ( જ્યાં $r$ એ બિંદુનો ઉદગમથી અંતર છે.). $20 \,cm$ ત્રિજ્યાના ગોળામાં ઉદગમ પાસે કેન્દ્રિત થયેલો વિદ્યુતભાર ................. $C$View Solution
- 4બંધ પૃષ્ઠની અંદરની બાજુએ $20\ \mu C$ નો વિદ્યુતભાર મૂકવામાં આવે તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ છે. જો $\, 80\ \mu C$ બંને વિદ્યુતભાર પૃષ્ઠની અંદરની બાજુએ ઉમેરવામાં આવે તો ફલક્સમાં થતો ફેરફાર....... છે.View Solution
- 5જો $\vec p$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલને નિયમિત વિદ્યુતક્ષેત્ર $\vec E$ માં મુક્તા તેના પર કેટલું ટોર્ક લાગશે?View Solution
- 6$ + 4q,\, - q$ અને $ + 4q$ વિદ્યુતભાર ધરાવતા બિંદુવત વિદ્યુતભારને $x - $અક્ષ પર $x = 0,\,x = a$ અને $x = 2a$ પર મૂકવામાં આવે તો ...View Solution
- 7બે બિંદુવત વિદ્યુતભારો $q_1$ અને $q_2$ હવામાં એકબીજાથી $50\, cm$ અંતરે આવેલા છે. અને અમુક ચોકકસ બળથી આંતરક્રિયા કરે છે હવે સમાન વિદ્યુતભારો જેની સાપેક્ષ પરિમિટિવિટિ $5$ હોય તેવા તેલમાં મૂકવામાં આવે છે. જો તેમના વચ્ચેનું આંતર બળ સમાન હોય તો તેલમાં અંતર ........ $cm$ છે.View Solution
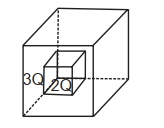
- 8આકૃતિતિાં દર્શાવ્યા અનુસાર $2 Q$ અને $3 Q$ જેટલો વિદ્યુતભાર ઘેરતા બે પોલા સમકેન્દ્રીય સમઘનો $C_1$ અને $C_2$ છે. $C_1$ અને $\mathrm{C}_2$ માંથી પસાર થતા વિદ્યુત ફ્લક્સનો ગુણોત્તર_____________છે.View Solution
- 9બે પાતળી ધાતુની પ્લેટ પર સમાન અને વિરુધ્ધ સંજ્ઞા ધરાવતી વિજભાર ઘનતા $(\sigma = 26.4 \times 10^{-12}\,c/m^2)$ છે.બે પ્લેટ વચ્ચે વિદ્યુતક્ષેત્ર કેટલું હશે?View Solution
- 10$10\,\mu C$ વીજભારને બે ભાગમાં વિભાજીત કરીને $1\,cm$ નાં અંતરે એવી રીતે મૂકવામાં આવે છે, કે જેથી તેના પર લાગતું અપાકર્ષી બળ મહત્તમ હોય. બે ભાગના વીજભાર ......... છે.View Solution
