બે બળોના સરવાળાનો પરિણામી સદિશ, તેના બાદબાકીના સદિશને લંબ છે. આ કિસ્સામાં બળો ..........
AIPMT 2003,AIIMS 2012, Medium
a
(a) If two vectors are perpendicular then their dot product must be equal to zero. According to problem
(a) If two vectors are perpendicular then their dot product must be equal to zero. According to problem
\((\overrightarrow A + \overrightarrow B ).(\overrightarrow A - \overrightarrow B ) = 0\)
\(⇒\) \(\overrightarrow A .\overrightarrow A - \overrightarrow A .\overrightarrow B + \overrightarrow B .\overrightarrow A - \overrightarrow B .\overrightarrow B = 0\)
\(⇒\)\({A^2} - {B^2} = 0\)
\(⇒\) \({A^2} = {B^2}\)
\(\therefore \) \(A = B\) i.e. two vectors are equal to each other in magnitude.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કાર $20\, m/s$ ની ઝડપથી ઉત્તર દિશામાં ગતિ કરે છે,તે વળાંક લઇને સમાન ઝડપથી પશ્વિમ દિશામાં ગતિ કરે,તો વેગમાં થતો ફેરફાર ..View Solution
- 2સમાન મૂલ્ય $R$ ધરાવતા બે સદીશો $\vec{A}$ અને $\vec{B}$ વચ્ચેનો ખૂણો $\theta$ છે તોView Solution
- 3બે સદીશો $\mathop A\limits^ \to \,$ અને $\mathop B\limits^ \to \,$ હોય તો , $\mathop A\limits^ \to \, + \mathop B\limits^ \to \,\,\, = \,\,\mathop C\limits^ \to $ અને ${A^2}\,\, + \;\,{B^2}\,\, = {C^2}$ છે . નીચેના માંથી ક્યું વિધાન સાચું છે .View Solution
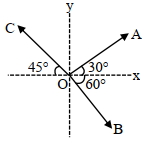
- 4આકૃતિમાં રહેલ સદિશ $\overrightarrow{ OA }, \overrightarrow{ OB }$ અને $\overrightarrow{ OC }$ ના મૂલ્ય સમાન છે. $\overrightarrow{ OA }+\overrightarrow{ OB }-\overrightarrow{ OC }$ ની $x$-અક્ષ સાથેની દિશા કેટલી થાય?View Solution
- 5$F$ અને $2F$ બળોનું પરિણામી એ $F$ ને લંબ છે.તો બે બળ વચ્ચેનો ખૂણો ........ $^o$ હશે.View Solution
- 6$A$ અને $\frac{A}{2}$ નાં મૂલ્યો ધરાવતા બે બળો એકબીજાને લંબ છે. તેનું પરિણામીનું મૂલ્ય ...... છે.View Solution
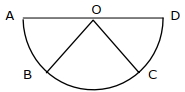
- 7વિધાન $A$ : જો $A, B, C, D$ એ અર્ધ વર્તુળ કેન્દ્ર $O$ પર ચાર બિંદુઓ એવા છે કે જેથી $|\overrightarrow{{AB}}|=|\overrightarrow{{BC}}|=|\overrightarrow{{CD}}|$ હોય, તો $\overrightarrow{{AB}}+\overrightarrow{{AC}}+\overrightarrow{{AD}}=4 \overrightarrow{{AO}}+\overrightarrow{{OB}}+\overrightarrow{{OC}}$View Solution
કારણ $R$ : સદીશ સરવાળાનો બહુકોણનો નિયમ $\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{A D}=2 \overrightarrow{A O}$ આપે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો પૈકી સૌથી વધારે યોગ્ય જવાબ પસંદ કરો.
- 8નીચેનામાંથી કઈ રાશિ/ રાશિઓ યામોક્ષોનાં અભિગમની પસંદગી પર આધાર રાખે છે?View Solution
$(a)$ $\vec{a}+\vec{b}$
$(b)$ $3 a_x+2 b_y$
$(c)$ $(\vec{a}+\vec{b}-\vec{c})$
- 9$A = \hat i + \hat j$ સદિશનો $X$ અક્ષ સાથે બનતો ખૂણો ......$^o$ હશે.View Solution
- 10જો સદિશ $(\hat a +2\hat b )$ એ સદિશ $(5 \hat a -4 \hat b )$ ને લંબ હોય તો , $\hat a $ અને $\hat b $ વચ્ચેનો ખૂણો ........ $^o$View Solution
