બે ગૂંચળાઓને જ્યારે સમાન ઉદ્દગમ સાથે જોડતાં સમાન ઉષ્મા ઉત્પન્ન કરવા માટે અનુક્રમે $20$ મીનીટ અને $60$ મીનીટ સમય લાગે છે. જે તેઓને સમાન ઉદ્દગમ સાથે સમાંતર ગોઠવણમાં જોડવામાં આવે તો સમાન પ્રમાણમાં ઉષ્મા ઉત્પન્ન કરવા માટ લાગતો સમય ........... મીનીટ હશે.
JEE MAIN 2022, Diffcult
b
\(\frac{d Q}{d t}=i^{2} R=\frac{V^{2}}{R}\) (we know)
\(\frac{d Q}{d t}=i^{2} R=\frac{V^{2}}{R}\) (we know)
\(\Rightarrow \text { In 't' time , } \Delta Q =\left(\frac{ V ^{2}}{ R }\right) t\)
Given that, (for same source, \(v=\) same)
\(Q _{0}=\frac{ v ^{2}}{ R _{1}} \times 20=\frac{ V ^{2}}{ R _{2}} \times 60 \ldots\) \((i)\)
\(\Rightarrow R _{2}=3 R _{1} \ldots.\) \((ii)\)
If they are connected in parallel then
\(\operatorname{Req}=\frac{ R _{2} R _{1}}{ R _{1}+ R _{2}}=\frac{3 R _{1} \cdot R _{1}}{3 R _{1}+ R _{1}}=\left(\frac{3 R _{1}}{4}\right)\)
To produce same heat, using equation ...\((i)\)
\(Q _{0}=\frac{ V ^{2}}{ R _{1}} \times 20=\frac{ v ^{2}}{\left(\frac{3 R _{1}}{4}\right)} \times t\)
\(t =\frac{3 \times 20}{4}=15 \,min\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન દ્રવ્ય અને સમાન લંબાઇ ધરાવતા બે તાર પરંતુ તેના આડછેદનો ગુણોત્તર $3:1$ છે. તેમને શ્રેણીમાં જોડેલ છે. જાડા તારનો અવરોધ $10\, \Omega$ છે. આ જોડાણનો સમતુલ્ય અવરોધ કેટલા .......... $\Omega$ થાય?View Solution
- 2મીટરબ્રીજમાં બે ગેપમાં અનુક્રમે $10\, \Omega$ અને $30 \,\Omega$ નાં અવરોધ છે. આ અવરોધોની અદલા બદલી કરતાં તટસ્થ બિંદુ.....સેમી ખસશે.View Solution
- 3$200\, {V}$ સ્ત્રોત ધરાવતા પરિપથ સાથે $100\, volt$ $500 \,watt$ નો ઇલેક્ટ્રિક બલ્બ જોડવામાં આવે છે. બલ્બને $500\, {W}$ નો પાવર આપવા માટે તેની સાથે શ્રેણીમાં કેટલો અવરોધ $R$ ($\Omega$) જોડાવો પડે?View Solution
- 4$\varepsilon\; emf$ અને $ r$ આંતરિક અવરોધનો એક કોષ ચલિત બાહ્ય અવરોધ $R$ સાથે જોડેલ છે. કયો આલેખ એ $R$ ની સાપેક્ષે કોષનો ટર્મિનલ વોલ્ટેજ $V $ આપે છે.View Solution
- 5$10 \mathrm{~cm}$ લંબાઈ અને $\sqrt{7} \times 10^{-4} \mathrm{~m}$ ત્રિજ્યા ના તારને મીટર બ્રીજના જમણા ગેપમાં જોડેલ છે.જ્યારે ડાબા ગેપમાં અવરોધ પેટી વડે $4.5 \Omega$ નો અવરોધ જોડવામાં આવે ત્યારે ડાબા છેડેથી $60 \mathrm{~cm}$ આગળ તટસ્થબિંદૂ (સંતુલન લંબાઈ) મળે છે.જો તારની અવરોધકતા $\mathrm{R} \times 10^{-7} \Omega \mathrm{m}$ હોય તો $\mathrm{R}$ નું મૂલ્ય_____છે.View Solution
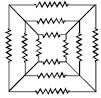
- 6બધા અવરોધનું મૂલ્ય $16 \,\Omega $ છે,તો બહારની ચોરસની એક બાજુ વચ્ચે સમતુલ્ય અવરોધ ......... $\Omega$View Solution
- 7વોલ્ટમીટરના માપાંકન(calibration) માં એક $ 1.1\,volt\,\, e.m.f$ ધરાવતા કોષને $440\,cm$ લંબાઈના તાર વહે સંતુલિત કરેલ છે. અવરોધ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત $220\,cm$ લંબાઈના તાર દ્વારા સંતુલિત થયેલ છે. તેને અનુરૂપ વોલ્ટમીટરનું અવલોકન $0.5\,volt$ મળે છે તો વોલ્ટમીટરના માપનમા કેટલા ................ $volt$ ત્રુટિ આવે?View Solution
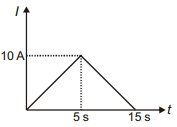
- 8સુવાહકમાંથી પસાર થતા વિદ્યુતપ્રવાહ $I$ વિરુદ્ધ સમય $t$ નો આલેખ આકૃતિમાં દર્શાવ્યા મુજબ છે. $0$ થી $15\,s$ ના અંતરાલમાં સુવાહકમાંથી પસાર થતો સરેરાશ વિદ્યુતપ્રવાહ $............ A$ છે.View Solution
- 9તારનો અવરોધ $50\,\Omega$ હોય તો $\log\,V$ અને $\log\,I$ વચ્ચેનો આલેખ........છે.View Solution
- 10View Solutionધરના પરિપથમાં બે બલ્બોમાં એક બલ્બ અન્ય કરતાં વધારે પ્રકાશિત છે. બંને બલ્બોમાંથી કયું બલ્બ વધારે અવરોધ ધરાવતું હશે ?
