બે કાર્નોટ એન્જિન $A$ અને $B$ ને શ્રેણીમાં એવી રીતે જોડવામાં આવે છે કે જેથી એન્જિન $A$ $T_{1}$ તાપમાનેથી ઉષ્માનું શોષણ કરીને $T$ ઠારણ વ્યવસ્થાના તાપમાને મુક્ત કરે છે. એન્જિન $B$ એન્જિન $A$ દ્વારા મુક્ત થતી ઉષ્માની અડધી ઉષ્માનું શોષણ કરીને તેને ${T}_{3}$ ઠારણ વ્યવસ્થાના તાપમાને મુક્ત કરે છે. જો બંને કિસ્સામાં કાર્ય સમાન હોય તો ${T}$ નું મૂલ્ય કેટલું હશે?
JEE MAIN 2021, Diffcult
Download our app for free and get started
a
carnot engine is as shown
carnot engine is as shown
\({W}_{{A}}=1-\frac{{Q}_{2}}{{Q}_{1}}=1-\frac{{T}}{{T}_{1}} \Rightarrow \frac{{Q}_{2}}{{Q}_{1}}=\frac{{T}}{{T}_{1}}\)
\({W}_{{B}}=1-\frac{{Q}_{3}}{\left({Q}_{2} / 2\right)}=1-\frac{{T}_{3}}{{T}} \Rightarrow \frac{2 {Q}_{3}}{{Q}_{2}}=\frac{{T}_{3}}{{T}}\)
Now, \({W}_{{A}}={W}_{{B}}\)
\({Q}_{1}-{Q}_{2}=\frac{{Q}_{2}}{2}-{Q}_{3}\)
\(\Rightarrow \frac{2 {Q}_{1}}{{Q}_{2}}+\frac{2 {Q}_{3}}{{Q}_{2}}=3\)
\(\Rightarrow \frac{2 {T}_{1}}{{T}}+\frac{{T}_{3}}{{T}}=3\)
\(\frac{2 {T}_{1}}{3}+\frac{{T}_{3}}{3}={T}\)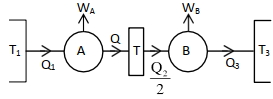
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionથરર્મોડાઇનેમિકસનો પ્રથમ નિયમ નીચે પૈકી કોની વિશેષ સ્થિતિ દર્શાવે છે?
- 2$27°C$ તાપમાને મોટરકારના ટાયરનું દબાણ $2$ વાતાવરણ દબાણ છે. જો ટાયર અચાનક ફાટી જતું હોય, તો તાપમાન ....... $K$ ( $\gamma = 1.4$ લો.)View Solution
- 3પિસ્ટન ઘરાવતા નળાકાર પાત્રમાં એક પરમાણ્વિક વાયુ $ {T_1}, $ તાપમાને ભરેલ છે. પિસ્ટનને અચાનક મુક્ત કરીને વાયુને સમોષ્મી રીતે ${T}_{2}$ તાપમાન સુધી વિસ્તરવા દેવામાં આવે છે. જો $l_{1}$ અને $l_{2}$ એ અનુક્રમે વિસ્તરણ પહેલા અને પછી વાયુના સ્થંભની લંબાઈ હોય તો $\frac{T_{1}}{T_{2}}$ નું મૂલ્ય કેટલું હશે?View Solution
- 4આદર્શ વાયુનું સમતાપી વિસ્તરણ કરતાં કદ $V_i$ થી $V_f$ અને દબાણ $P_i$ થી $P_f$ થાય તો વાયુ પર કેટલું કાર્ય થયું હશે?View Solution
- 5$5.6$ લીટર હિલિયમને $ STP$ એ સમોષ્મી રીતે $0.7$ લીટર સુધી સંકોચવામાં આવે છે. પ્રારંભીક તાપમાન $T_1$ લેતા પ્રક્રિયા દરમિયાન થતુ કાર્ય...?View Solution
- 6સામાન્ય દબાણે $(1.013 \times 10^5\ Nm^{-2} ) $ અને $100 ^o C$ પર પાણીના એક નમુનાને $100\ ^o C$ પર $0.1\ g$ વરાળમાં ફેરવવા માટે $54\ cal$ ઉષ્મા ઊર્જાની જરૂર પડે છે. જો ઉત્પન્ન થતી વરાળનું કદ $167.1\ cc$ છે, તો આ નમુનાની આંતરિક ઊર્જામાં થતો ફેરફાર ...... $J$ છે.View Solution
- 7$-10^{\circ} {C}$ થી $25^{\circ} {C}$ વચ્ચે કાર્ય કરતું રેફ્રિજરેટર સરેરાશ $35\, {W}$ નો પાવર વાપરે છે. જો તેમાં કોઈ પણ પ્રકારનો ઉર્જાનો વ્યય થતો ના હોય તો દર સેકન્ડે તે સરેરાશ કેટલી ઉષ્માનું (${J} / {s}$) વહન કરશે?View Solution
- 8એક કાર્નોટ એન્જિન $627°$ તાપમાને પ્રાપ્તિસ્થાનમાંથી $3 × 10^{6} cal$ ઉષ્મા શોષે છે અને $27°C $ તાપમાને મુક્ત કરે છે, તો એન્જિન વડે થયેલું કાર્ય .......View Solution
- 9એક આદર્શ વાયુ $P^2 V=$ અચળ નિયમને અનુરૂપ વિસ્તરણ પામે છે. વાયુની આંતરિક ઊર્જા...View Solution
- 10$27\,^oC$ ઓરડાના તાપમાને રહેલ એક મોલ એક પરમાણ્વિક આદર્શ વાયુનું સંકોચન કરી તેનું દબાણ બમણું કરવા કેટલું કાર્ય કરવું પડે?View Solution