બે લંબ રીતે સરળ આવર્ત ગતિ કરતાં પદાર્થ માટે સમીકરણ નીચે આપેલા છે.તેમને જોડીને Lissajous ગ્રાફ બનાવવામાં આવે છે.
$x\left( t \right) = A\,\sin \,\left( {at + \delta } \right)$
$y\left( t \right) = B\,\sin \,\left( {bt} \right)$
તો નીચેનામાંથી શું સાચું પડશે?
JEE MAIN 2018, Diffcult
Download our app for free and get started
c
From the two mutually perpendicular \(S.H.M. 's\), the general equation of Lissajous figure \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{y^2}}}{{{B^2}}} - \frac{{2xy}}{{AB}}\cos \,\delta = {\sin ^2}\,\delta\) \(x = A\,\sin \,\left( {at + \delta } \right)\) \(y = B\,\sin \,\left( {bt + r} \right)\) Clearly \(A\ne B\) hence ellipse
From the two mutually perpendicular \(S.H.M. 's\), the general equation of Lissajous figure \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{y^2}}}{{{B^2}}} - \frac{{2xy}}{{AB}}\cos \,\delta = {\sin ^2}\,\delta\) \(x = A\,\sin \,\left( {at + \delta } \right)\) \(y = B\,\sin \,\left( {bt + r} \right)\) Clearly \(A\ne B\) hence ellipse
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$ x = a\sin \left( {\omega t + \frac{\pi }{6}} \right) $ અને $ x' = a\cos \omega t $ સરળ આવર્ત ગતિ વચ્ચે કળા તફાવત કેટલો થાય?View Solution
- 2એક સમક્ષિતિજ સ્પ્રિંગ સાથે જોડેલ $M$ દળનો પદાર્થ $A _{1}$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે. જ્યારે $M$ દળનો પદાર્થ મધ્યમાન સ્થાન પરથી પસાર થાય છે. ત્યારે તેના પર $m$ દળનો નાનો પદાર્થ મૂકવામાં આવે છે અને બંને પદાર્થો $A_{2}$ જેટલા કંપવિસ્તારથી સરળ આવર્તગતિ કરે છે, તો $\frac{A_{1}}{A_{2}}$ કેટલો થાય?View Solution
- 3સરળ આવર્તગતિની કુલઊર્જા $E$ છે.તો અડધા કંપવિસ્તારે ગતિઊર્જા કેટલી થાય?View Solution
- 4સરળ આવર્ત ગતિ કરતાં કણ માટે મહત્તમ પ્રવેગ અને વેગનો ગુણોત્તર $10\,s^{-1}$ છે. $t = 0$ સમયે તેનું સ્થાનાંતર $5\, m$ હોય તો તેનો મહત્તમ પ્રવેગ કેટલો હશે? શરૂઆતની કળા $\frac{\pi }{4}$ છે.View Solution
- 5સરળ આવર્તગતિ $x = a\sin (\omega \,t - \alpha )$ અને $y = b\cos (\omega \,t - \alpha )$ ની વચ્ચે કળા તફાવત કેટલો થશે?View Solution
- 6$x$ અક્ષ પર ગતિ કરતાં $100 \,g$ પદાર્થની સ્થિતિ ઊર્જા $U=5 x(x-4)$ વડે દર્શાવાય છે. જ્યારે $x$ મીટરમાં છે, આ દોલનનો આવર્તકાળ શોધો.View Solution
- 7$20 \,cm$ નાં સરખા કંપવિસ્તાર, સરખા આવર્તકાળ સાથે એક જ મધ્યબિંદુ આસપાસ એક જ રેખા પર બે કણ ગતિ કરે છે. જો તેમની વચ્ચેનું મહત્તમ અંતર $20 \,cm$ હોય, તો તેમની કળાનો તફાવત કેટલા રેડિયન જેટલો થશે ?View Solution
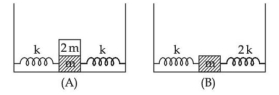
- 8આકૃતિ $(A)$ માં ‘$2\,m$’ દળને ' $m$ ' દળ ઉપર જડવામાં આવ્યો છે. $m$ દળ $k$ જેટલો સ્પ્રિંગ અચળાંક ઘરાવતી સ્પ્રિંગો સાથે જોડવામાં આવેલ છે. આકૃતિ $(B)$ માં ‘ $m$ ' દળને ' $k$ ' અને ‘ $2 k$ ' સ્ત્રિંગ અચળાંકો ઘરાવતી બે સ્પ્રિંગો સાથે જ્રેડવામાં આવેલ છે. જે $(A)$ માં દળ ' $m$ ' ને અને $(B)$ માં દળ ' $m$ ' ને ' $x$ ' અંતરે ખસેડવામાં આવે તો, $(A)$ અને $(B)$ ને અનુરૂપ આવર્તકાળ $T _1$ અને $T _2........$ સમીકરણને અનુસરશે.View Solution
- 9$0.05$ મી કંપ વિસ્તાર ધરાવતી સરળ આવર્ત ગતિનું સ્થાનાંતર $0.01$ મી હોય ત્યારે પ્રવેગ $1.0 \,m / s ^{2}$ છે,તો તેનો આવર્તકાળ કેટલો હશે?View Solution
- 10સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $ x = A\cos \left( {\omega t + \frac{\pi }{4}} \right) $ છે.તેનો મહત્તમ વેગ કયાં સમયે થશે?View Solution