બે પદાર્થ $A$ અને $B$ ની ઉત્સર્જકતા $0.01$ અને $0.81$ છે.બંને પદાર્થના સપાટીના ક્ષેત્રફળ સમાન અને ઉત્સર્જન પાવર સમાન છે.જો $A$ પદાર્થનું તાપમાન $ 5802\;K $ હોય,તો $B$ પદાર્થનું તાપમાન કેટલું હોવું જોઈએ.
IIT 1994, Diffcult
d
(d) According to Stefan’s law
\(E = eA\sigma {T^4} \Rightarrow {E_1} = {e_1}A\sigma T_1^4\) and \({E_2} = {e_2}A\sigma T_2^4\)
\({E_1} = {E_2}\) \(\therefore \)\({e_1}T_1^4 = {e_2}T_2^4\)
\( \Rightarrow \)\({T_2} = {\left( {\frac{{{e_1}}}{{{e_2}}}T_1^4} \right)^{\frac{1}{4}}} = {\left( {\frac{1}{{81}} \times {{(5802)}^4}} \right)^{\frac{1}{4}}}\)\( \Rightarrow \)\({T_B} = 1934\;K\)
And, from Wein’s law \({\lambda _A} \times {T_A} = {\lambda _B} \times {T_B}\)
\( \Rightarrow \frac{{{\lambda _A}}}{{{\lambda _B}}} = \frac{{{T_B}}}{{{T_A}}}\)\( \Rightarrow \)\(\frac{{{\lambda _B} - {\lambda _A}}}{{{\lambda _B}}} = \frac{{{T_A} - {T_B}}}{{{T_A}}}\)
\( \Rightarrow \)\(\frac{1}{{{\lambda _B}}} = \frac{{5802 - 1934}}{{5802}} = \frac{{3968}}{{5802}} \Rightarrow {\lambda _B} = 1.5\;\mu m\)
(d) According to Stefan’s law
\(E = eA\sigma {T^4} \Rightarrow {E_1} = {e_1}A\sigma T_1^4\) and \({E_2} = {e_2}A\sigma T_2^4\)
\({E_1} = {E_2}\) \(\therefore \)\({e_1}T_1^4 = {e_2}T_2^4\)
\( \Rightarrow \)\({T_2} = {\left( {\frac{{{e_1}}}{{{e_2}}}T_1^4} \right)^{\frac{1}{4}}} = {\left( {\frac{1}{{81}} \times {{(5802)}^4}} \right)^{\frac{1}{4}}}\)\( \Rightarrow \)\({T_B} = 1934\;K\)
And, from Wein’s law \({\lambda _A} \times {T_A} = {\lambda _B} \times {T_B}\)
\( \Rightarrow \frac{{{\lambda _A}}}{{{\lambda _B}}} = \frac{{{T_B}}}{{{T_A}}}\)\( \Rightarrow \)\(\frac{{{\lambda _B} - {\lambda _A}}}{{{\lambda _B}}} = \frac{{{T_A} - {T_B}}}{{{T_A}}}\)
\( \Rightarrow \)\(\frac{1}{{{\lambda _B}}} = \frac{{5802 - 1934}}{{5802}} = \frac{{3968}}{{5802}} \Rightarrow {\lambda _B} = 1.5\;\mu m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$l (x = 0$ થી $ x = l )$ લંબાઇના વાહકમાંથી ઉષ્મા પસાર થાય છે.તો તાપમાન વિરુધ્ધ અંતરનો આલેખView Solution
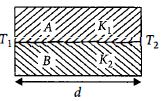
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે જુદા-જુદા દ્રવ્યમાંથી બનેલા બે સળિયા $A$ અને $B$ ને એકસાથે વેલ્ડ કરવામાં આવે છે. આ સળિયાઓની ઉષ્મા વાહકતા અનુક્રમે $K _{1}$ અને $K _{2}$ છે. બનેલા સંયુક્ત સળિયાની ઉષ્મા વાહકતા કેટલી થાય?View Solution
- 3બે તારામાંથી આવતા પ્રકાશની મહત્તમ તરંગલંબાઇ $ 510\;nm $ અને $ 350\;nm $ છે.તો તેના તાપમાનનો ગુણોત્તર કેટલો થાય?View Solution
- 4જો $e_\lambda$ અને $a_\lambda$ એ અનુક્રમે પદાર્થનો ઉત્સર્જન પાવર અને શોષણ પાવર છે અને $E_\lambda$ એ સંપૂર્ણ કાળા પદાર્થનો ઉત્સર્જન પાવર કિર્ચોફના નિયમ પ્રમાણે શું થશે?View Solution
- 5તળાવની ઉપરની સપાટીનું તાપમાન $2^{\circ} C$ છે તો તેના તળીયાનું તાપમાન ............ $^{\circ} C$ હોયView Solution
- 6જયારે સંપૂર્ણ કાળા પદાર્થનું તાપમાન વધારવામાં આવે છે ત્યારે $\lambda_m$ નું મૂલ્ય $0.26 \mu_m$ થી $0.13 \mu_m$ નો ફેરફાર અનુભવે છે તો આ તાપમાનને અનુલક્ષિને તેની ઉત્સર્જન પાવરનો ગુણોત્તર ……View Solution
- 7સૂર્યને $T\; K$ તાપમાને $R$ ત્રિજ્યાનાં ગોળા તરીકે ધારતાં, સૂર્યમાંથી પૃથ્વી પર આપાત થતો કુલ ઉત્સર્જન પાવર ગણો. પૃથ્વીનું સૂર્યથી અંતર $r$ લો.View Solution
જ્યાં $r_{0}$ એ પૃથ્વીની ત્રિજ્યા અને $\sigma$ એ સ્ટીફન અચળાંક છે.
- 8સૂર્યને $T\; K$ તાપમાને $R$ ત્રિજ્યાનાં ગોળા તરીકે ધારતાં, સૂર્યમાંથી પૃથ્વી પર આપાત થતો કુલ ઉત્સર્જન પાવર ગણો. પૃથ્વીનું સૂર્યથી અંતર $r$ લો.View Solution
જ્યાં $r_{0}$ એ પૃથ્વીની ત્રિજ્યા અને $\sigma$ એ સ્ટીફન અચળાંક છે.
- 9View Solutionસમાન દ્રવ્ય અને સમાન કદ ઘરાવતી એક ગોળા અને સમઘનને સમાન તાપમાન સુઘી ગરમ કરવામાં આવે છે.અને સમાન વાતાવરણમાં ઠંડા પાડવા દેવામાં આવે ત્યારે તેમના ઉત્સર્જન પાવરનો ગુણોતર કેટલો થાય?
- 10કાળો પદાર્થ $2880\;K$ તાપમાને છે.આ પદાર્થ તરંગલંબાઈ $499\;nm$ થી $500\;nm$ ની વચ્ચે ${U_1}$ ઉર્જાનું ઉત્સર્જન $999\;nm$ થી $1000\;nm$ ની વચ્ચે ${U_2}$ ઉર્જાનું ઉત્સર્જન અને $1499\;nm$ થી $1500\;nm$ ની વચ્ચે ${U_3}$ ઉર્જાનું ઉત્સર્જન કરે તો..... (વીનનો અચળાંક $b = 2.88 \times {10^6}\;nm\,K$).View Solution
