બે પ્લેટ વચ્ચેનું અંતર $d$ ધરાવતા સમાંતર પ્લેટ કેપેસીટરમાં $\frac{3}{4} d$ જાડાઈ અને $K$ ડાઈઇલેક્ટ્રિક અચળાંક ધરાવતો સ્લેબ મૂકવામાં આવે છે તો નવો કેપેસીટન્સ $(C')$ અને જૂના કેપેસીટન્સ $\left( C _{0}\right)$ વચ્ચેનો સંબંધ શું થશે?
JEE MAIN 2021, Medium
Download our app for free and get started
c
\(C _{0}=\frac{\epsilon_{0} A }{ d }\)
\(C _{0}=\frac{\epsilon_{0} A }{ d }\)
\(C ^{\prime}= C _{1}\) and \(C _{2}\) in series.
i.e. \(\frac{1}{ C ^{\prime}}=\frac{1}{ C _{1}}+\frac{1}{ C _{2}}\)
\(\frac{1}{ C ^{\prime}}=\frac{(3 d / 4)}{\epsilon_{0} KA }+\frac{ d / 4}{\epsilon_{0} A }\)
\(\frac{1}{ C ^{\prime}}=\frac{ d }{4 \epsilon_{0} A }\left(\frac{3+ K }{ K }\right)\)
\(C ^{\prime}=\frac{4 K C _{0}}{(3+ K )}\)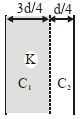
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સમબાજુ ત્રિકોણનાં શિરોબિંદુઓ પર અનુક્રમે $q,q$ અને $-2 q$ જેટલો વિદ્યુતભાર રાખેલ છે. સમબાજુ ત્રિકોણની બાજુની લંબાઈ $L$ છે. કોઈપણ પ્રકારની પ્રવેગરહિત ગતિ દ્વારા આા ત્રણેય વિદ્યુતભારને એકબીજાથી દૂર કરવા માટે બાહ્ય ચાર્જ દ્વારા કરવામાં આવતું કાર્ય કેટલું થશે?View Solution
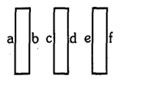
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $A$ ક્ષેત્રફળ ધરાવતી દરેક ત્રણ સમાંતર ધાતુની પ્લેટો મુકેલી છે અને $Q_1$, $Q_2$ અને $Q_3$ વિદ્યુતભારો તેઓને આપવામાં આવે છે. છેડા (ધાર) પરની અસરો નગણ્ય છે. તો સૌથી બહારની બે સપાટીઓ $'a'$ અને $'f'$ પરનો વિદ્યુતભાર ગણો.View Solution
- 3બે બિંદુઓ $P$ અને $Q$ આગળ વિદ્યુતસ્થિતિમાનમાં મૂલ્યો અનુક્રમે $10\; V$ અને $-4 \;V$ છે. તો $100$ ઈલેક્ટ્રોનને બિંદુ $P$ થી $Q$ પર લાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
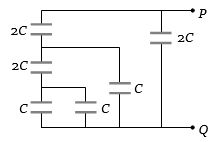
- 4View Solutionઆપેલ પરિપથનો સમતુલ્ય કેપેસીટન્સ કેટલો થાય?
- 5$C_1 = 1\,\mu F$ કેપેસિટરને મહતમ $V_1 = 6\, KV$ અને $C_2 = 3\,\mu F$ કેપેસિટરને મહતમ $V_2 = 4\,KV$ વોલ્ટેજ આપી શકીએ છીએ. જો બંને કેપેસિટરને શ્રેણીમાં લગાવીએ તો તેને મહતમ કેટલા........$KV$ વોલ્ટેજ આપવા જોઇએ?View Solution
- 6એક કેપેસીટરને ચાર્જ કરવા માટે એક બેટરી $200\,J$ જેટલું કાર્ય કરે છે. તેથી કેપેસીટરમાં સંગ્રહિત ઉર્જા $.......J$ હશે.View Solution
- 7$m$ દળવાળા અને $e$ વિદ્યુતભાર ધરાવતા ઇલેકટ્રોનને સ્થિર સ્થિતિમાંથી $V$ જેટલા વોલ્ટેજે શૂન્યાવકાશમાં પ્રવેગિત કરવામાં આવે છે, તો ઇલેકટ્રોનનો અંતિમ વેગ કેટલો હશે?View Solution
- 8કેપેસીટરને $10\, \Omega$ ના અવરોધ દ્વારા $20\, {V}$ ની બેટરી સાથે જોડેલ છે. એવું જાણવા મળ્યું છે કે કેપેસિટર પરનો વોલ્ટેજ $1\, \mu {s}$ માં $2\, {V}$ જેટલો વધે છે. કેપેસીટર પરનો કેપેસીટન્સ ($\mu {F}$ માં) કેટલો હશે? આપેલ : $\ln \left(\frac{10}{9}\right)=0.105$View Solution
- 9નીચેના વિધાન $-1$ અને વિધાન $-2$ વાંચીને યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $-1$ : એક વિદ્યુતભારિત કણ $P$ થી $Q$ તરફ ગતિ કરે છે. આ દરમિયાન વિદ્યુતક્ષેત્ર દ્વારા કણ પર થતું કાર્ય એ $P$ થી $Q$ તરફના ગતિમાર્ગ પર આધારિત નથી.
વિધાન $-2$ : બંધ માર્ગમાં ગતિ કરતાં કણ પર સંરક્ષી બળ વડે થતું કાર્ય શૂન્ય હોય છે.
- 10નીચેના વિધાન $-1$ અને વિધાન $-2$ વાંચીને યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $-1$ : એક વિદ્યુતભારિત કણ $P$ થી $Q$ તરફ ગતિ કરે છે. આ દરમિયાન વિદ્યુતક્ષેત્ર દ્વારા કણ પર થતું કાર્ય એ $P$ થી $Q$ તરફના ગતિમાર્ગ પર આધારિત નથી.
વિધાન $-2$ : બંધ માર્ગમાં ગતિ કરતાં કણ પર સંરક્ષી બળ વડે થતું કાર્ય શૂન્ય હોય છે.