બે સદિશ $\vec X$ અને $\vec Y$ સમાન માન ધરાવે છે. $(\vec X - \vec Y)$ નું માન એ $(\vec X + \vec Y)$ ના માન કરતા $n$ ગણું છે. $\vec X$ અને $\vec Y$ વચ્ચેનો ખૂણો કેટલો હશે?
JEE MAIN 2021, Diffcult
b
Given \(X=Y\)
Given \(X=Y\)
\(\sqrt{ X ^{2}+ Y ^{2}-2 \times Y \cos \theta}\)
\(= n \sqrt{ X ^{2}+ Y ^{2}+2 \times Y \cos \theta}\)
Square both sides
\(2 X ^{2}(1-\cos \theta)= n ^{2} \cdot 2 X ^{2}(1+\cos \theta)\)
\(1-\cos \theta= n ^{2}+ n ^{2} \cos \theta\)
\(\cos \theta=\frac{1- n ^{2}}{1+ n ^{2}}\)
\(\theta=\cos ^{-1}\left[\frac{ n ^{2}-1}{- n ^{2}-1}\right]\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$P\,\, = \,\,{\rm{Q}}\,\, = \,\,{\rm{R}}$ જો $\mathop {\,{\rm{P}}}\limits^ \to \,\, + \;\,\mathop {\rm{Q}}\limits^ \to \,\, = \,\,\mathop {\rm{R}}\limits^ \to \,$ હોય તથા $\mathop {\rm{P}}\limits^ \to $ અને $\mathop {\rm{R}}\limits^ \to $ વચ્ચેનો ખૂણો ${\theta _1}$ છે. જો $\mathop {\rm{P}}\limits^ \to \,\, + \;\,\mathop {\rm{Q}}\limits^ \to \,\, + \,\,\mathop {\rm{R}}\limits^ \to \,\, = \,\,\mathop {\rm{0}}\limits^ \to $ હોય તો $\mathop {\rm{P}}\limits^ \to $ અને $\mathop {\rm{R}}\limits^ \to $ વચ્ચેનો ખૂણો ${\theta _2}$ છે. ${\theta _1}$ અને ${\theta _2}$ વચ્ચેનો સંબંધ શું કહે ?View Solution
- 2${\rm{\hat i}}\,\,{\rm{ - }}\,\,{\rm{\hat j}}\,\, + \;\,{\rm{\hat k}}\,$ અને $\,{\rm{\hat i}}\,\, + \,\,{\rm{\hat j}}\,\, + \;\,{\rm{\hat k}}$ બે સદીશોનો એકમ લેબં સદીશ શોધો .View Solution
- 3$a$ બાજુ ધરાવતા ઘનમાં, ફલક (સપાટી) $ABOD$ ના કેન્દ્ર આગળથી ફલક $BEFO$ ના કેન્દ્ર સુધી (આકૃતિમાં દર્શાવ્યા અનુસાર) દોરેલ સદિશ કયો હશે.View Solution
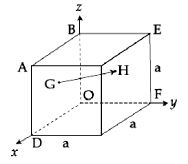
- 4$ABC$ એ સમબાજુ ત્રિકોણ છે. દરેક બાજુની લંબાઈ $'a'$ અને તેનું પરિકેન્દ્ર $O$ છે. $\overrightarrow{A B}+\overrightarrow{A C}=n \overrightarrow{A O}$ હોય તો $n = $ ........View Solution
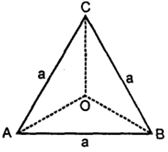
- 5સદિશ $ \overrightarrow A $ , $x, y$ અને $z$ સાથે સમાન ખૂણો બનાવે છે. તો તે સદિશના ઘટકનું મૂલ્ય કેટલું હોય?View Solution
- 6જો $\vec{A}=(2 \hat{i}+3 \hat{j}-\hat{k})\; m$ અને $\vec{B}=(\hat{i}+2 \hat{j}+2 \hat{k}) \;m$ છે. સદિશ $\vec{A}$ નો સદિશ $\vec{B}$ ની દિશામાંના ધટકનું મૂલ્ય $.....m$ થશે.View Solution
- 7જો $ |\vec A \times \vec B| = \sqrt 3 \vec A.\vec B $ હોય, તો $ |\vec A + \vec B| $ નું મૂલ્ય શું થાય?View Solution
- 8એક પ્લેન $100 \,km/hr$ ની ઝડપથી પૃથ્વીને ફરતે પરિભ્રમણ કરે છે.તે અડધું પરિભ્રમણ કરે,ત્યારે તેના વેગમાં કેટલો ફેરફાર ......... $km/hr$ થાય?View Solution
- 9જો $| A + B |=| A |+| B |$ હોય તો સદિશ $ \overrightarrow A $ અને $ \overrightarrow B $ વચ્ચેનો ખૂણો કેટલો હોવો જોઈએ?View Solution
- 10ક્યાં સદિશને પરિણામી સદિશ $\mathop P\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,7\hat j\,\, - \,\,10\hat k\,\,$ અને $\,\,\mathop Q\limits^ \to \,\, = \,\,\hat i\,\, + \;\,2\hat j\,\, + \;\,3\hat k$ માં ઉમેરવામાં આવે તો તે $X$- અક્ષની દિશામાં એકમ સદિશ આપે.View Solution
