બે સમાન અને વિરૂદ્ધ વિજભારો અને જોડતી રેખાના સમચેદી ના કોઈ પણ બિંદુ આગળ.......
Easy
b
Electric field at \(P\) due \((-q)\) will be in direction \(P B\) given by \(E_1\)
Electric field at \(P\) due \((-q)\) will be in direction \(P B\) given by \(E_1\)
\(E_1=\frac{1}{4 \pi \varepsilon_0}+\frac{q}{\sqrt{x^2+a^2}}(\cos \theta \hat{\imath}+\sin \theta \hat{\jmath})\)
Fectric field at \(p\) due \((+2)\) will be
\(E_2=\frac{1}{4 \pi t_0} \frac{q}{\sqrt{x^2+a^2}}(\cos \hat{\imath}-\sin \theta \hat{\jmath})\)
Total Electric field \(t E=E_1+E_2\)
\(E =\frac{1}{4 \pi \epsilon_0} \frac{2}{\sqrt{x^2+q^2}}\left[2 \cos \theta \hat{\imath}+\sin \theta \hat{\jmath}-\sin \theta e_{ l }\right]\)
\(=\frac{2 q 2 \cos \theta \hat{\imath}}{4 \pi \epsilon_0 \sqrt{x^2+q^2}}\)
Total potential will be \(v=v_1+r_2\)
\(V=\frac{1}{4 \pi t_0} \frac{q}{\sqrt{x^2+a^2}}-\frac{1}{4 \pi t_0} \frac{q}{\sqrt{x^2+a^2}}=0\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$4\ \mu \,F$ કેપેસિટરને $400\ V$ વોલ્ટથી ચાર્જ કરીને અવરોધ $1\,k\Omega $ સાથે જોડવામાં આવે છે. તો કેટલા ........$J$ ઉષ્મા ઉત્પન્ન થાય?View Solution
- 2${10^{ - 10}}\,m$ અંતરે રહેલા બે પ્રોટ્રોનને મુકત કરતાં અનંત અંતરે ગતિઊર્જા કેટલી થાય?View Solution
- 3એક સમાંતર પ્લેટ કેપેસિટરની પ્લેટનું ક્ષેત્રફળ $A,$ તેનું કેપેસિટન્સ $C$ અને પ્લેટો વચ્ચેનું અંતર $d$ છે.જેમાં $K_1,K_2,K_3$ અને $K_4$ ડાઇઇલેકિટ્રક અચળાંકવાળા ચાર ડાઇઇલેકિટ્રકોના આકૃતિમાં દર્શાવ્યા પ્રમાણે ભરેલાં છે.જો કોઇ એક જ ડાઇઇલેકિટ્રક પદાર્થને વાપરતાં તેટલું જ કેપેસિટન્સ $ C$ મળે,તો ડાઇઇલેકિટ્રક અચળાંક $ K=$ ________View Solution
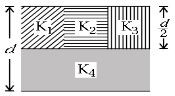
- 4ડિફાઈબ્રીલેટરમાં $40\ \mu F$ કેપેસિટરને $3000\, V$ સુધી વિદ્યુતભારિત કરેલ છે.$2$ મિ.લિ સેંકડ અવધિના સ્પંદ દરમિયાન કેપેસિટરની સંગ્રહિત ઉર્જાને દર્દીં મારફતે મોકલવામાં આવે તો તે દર્દીંને આપવામાં આવેલ પાવર કેટલા ........$kW$ છે ?View Solution
- 5ઋણ વિદ્યુતભાર કરેલી પ્લેટ પર ઋણ વિદ્યુતભાર ઘનતા $2 \times 10^{-6}\ C/m^2$ છે તો હવે $200\ eV$ ઊર્જા ધરાવતો એક ઇલેક્ટ્રોન પ્લેટ તરફ ગતી કરે છે પરંતુ પ્લેટને અથડાતો નથી તો તેનું પ્લેટથી પ્રારંભીક અંતર........$mm$ શોધો.View Solution
- 6બે વિદ્યુતભારો $4 × 10^{-8}\ C $ અને $-6 × 10^{-8} $ $C$ અને $B$ આગળ મૂકેલા છે. જે $50 \,cm$ જેટલા દૂર છે. $AB$ રેખા પર બિંદુ $A$ થી કયા.....$cm$ ના બિંદુ આગળ વિદ્યુત સ્થિતિમાન શૂન્ય છે?View Solution
- 7$10^{-6} \mu \mathrm{C}$ નો એક વીજભાર $X-Y$ યામ પધ્ધતિના ઉગમબિંદુ $(0,0) \mathrm{m}$ પર મૂકેલો છે. બિંદુઓ $\mathrm{P}$ અને $\mathrm{Q}$ અનુક્રમે $(\sqrt{3}, \sqrt{3}) \mathrm{m}$ અને $(\sqrt{6}, 0) \mathrm{m}$ પર રહેલા છે. બિંદુઓ$\mathrm{P}$ અને $\mathrm{Q}$ વચચેનો સ્થિતિમાન તફાવત_____થશે.View Solution
- 8એક સમાંતર પ્લેટ કેપેસિટરની પ્લેટનું ક્ષેત્રફળ $A,$ તેનું કેપેસિટન્સ $C$ અને પ્લેટો વચ્ચેનું અંતર $d$ છે.જેમાં $K_1,K_2,K_3$ અને $K_4$ ડાઇઇલેકિટ્રક અચળાંકવાળા ચાર ડાઇઇલેકિટ્રકોના આકૃતિમાં દર્શાવ્યા પ્રમાણે ભરેલાં છે.જો કોઇ એક જ ડાઇઇલેકિટ્રક પદાર્થને વાપરતાં તેટલું જ કેપેસિટન્સ $ C$ મળે,તો ડાઇઇલેકિટ્રક અચળાંક $ K=$ ________View Solution
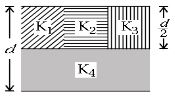
- 9એક સંધારક $R$ અવરોધની મદદથી વિદ્યુતભાર રહિત (ડીસ્ચાર્જ) થાય છે. ધારો કે $t_{1}$ સમયમાં સંધારકમાં સંગ્રહીત ઊર્જા ધટીને તેની પ્રારંભિક મૂલ્ય કરતાં અડધી થાય છે અને $t _{2}$ સમયમાં સંગ્રહીત વિદ્યુતભાર ધટીને તેનાં પ્રારંભિક મૂલ્ય કરતા આઠમા ભાગનો થાય છે. $t_{1} / t_{2}$ ગુણોત્તર .............થશે.View Solution
- 10બે એક સરખા કેપેસીટર સમાન કેપેસીટન્સ (સંધારકતા) ધરાવે છે. તેમાનાં એકને $V$ સ્થિતિમાન વડે અને બીજાને $2 V$ સ્થિતિમાન વડે વીજભારિત કરવામાં આવે છે. બંનેના ઋણ છેડાને જોડેલા છે જયારે તેમના ધન છેડાઓને પણ જોડવામાં આવે ત્યારે સંયુક્ત તંત્રની ઊર્જામાં થતો ઘટાડો______છે.View Solution
