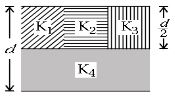
Here, \(C_{1}=\frac{2 \varepsilon_{0} k_{1} A}{3 d}, C_{2}=\frac{2 \varepsilon_{0} k_{2} A}{3 d}\)
\(C_{3}=\frac{2 \varepsilon_{0} k_{3} A}{3 d}, C_{4}=\frac{2 \varepsilon_{0} k_{4} A}{d}\)
Given system of \(C_{1}, C_{2}, C_{3}\) and \(C_{4}\) can be simplified as \(\therefore \frac{1}{C_{A B}}=\frac{1}{C_{1}+C_{2}+C_{3}}+\frac{1}{C_{4}}\)
Suppose, \(C_{A B}=\frac{k \varepsilon_{0} A}{d}\)
\(\quad \frac{1}{k\left(\frac{\varepsilon_{0} A}{d}\right)}=\frac{1}{\frac{2}{3} \frac{\varepsilon_{0} A}{d}\left(k_{1}+k_{2}+k_{3}\right)}+\frac{1}{\frac{2 \varepsilon_{0} A}{d} k_{4}}\)
\(\Rightarrow \frac{1}{k}=\frac{3}{2\left(k_{1}+k_{2}+k_{3}\right)}+\frac{1}{2 k_{4}} \therefore \frac{2}{k}=\frac{3}{k_{1}+k_{2}+k_{3}}+\frac{1}{k_{4}}\)
Download our appand get started for free
Similar Questions
- 1$a$ અને $b$ (જ્યાં $a < b)$ ત્રિજ્યાઓ ધરાવતા ગોળાઓ $A$ અને $B$ એકબીજાથી ખૂબ જ લાંબા અંતરે છે.બંને ગોળાઓ પર $100\,\mu C$ જેટલો ચાર્જ રહેલ છે, જો બંને ગોળાઓને વાહક તાર વડે જોડવામાં આવે તો નીચેનામાંથી ક્યું પરીણામ મળે?View Solution
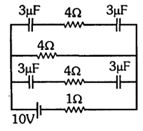
- 2આપેલા પરિપથ માટે, સ્થિર સ્થિતિમાં દરેક કેપેસિટરનો વિદ્યુતભાર.......$\mu C$ ગણો.View Solution
- 3સમાંતર પ્લેટ કેપેસીટરની પ્લેટ વચ્ચે ડાઈઇલેક્ટ્રિક મૂકવામાં આવે છે. જેનો ડાઈઇલેક્ટ્રિક અચળાંક નીચે મુજબ બદલાય છે.View Solution
$K(x) = K_0 + \lambda x$ ($\lambda =$ અચળાંક)
શૂન્યાવકાશમાં કેપેસીટરનું મૂલ્ય $C_0$ હોય તો $C_0$ના સ્વરૂપમાં કેપેસીટન્સ $C$ કેટલું મળે?
- 4આપેલ પરિપથમાં, છેડા $A$ અને છેડા $B$ વચ્ચે સમતુલ્ય સંધારકતાView Solution
. . . . . . .છે
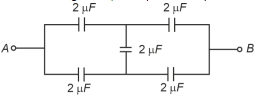
- 5$2\mu F$ કેપેસિટેન્સ ધરાવતા સાત કેપેસિટરોને એવી સંરચના વડે જોડવામાં આવે છે કે જેથી તેનો અસરકારક કેપેસિટન્સ $\left( {\frac{6}{{13}}} \right)\,\mu F$ મળે. નીચેની આકૃતીમાંથી ક્યું સંયોજન જરૂરી મૂલ્ય આપે છે?View Solution
- 6બે બિંદુવત ડાયપોલ ${\vec P_1}$ અને ${\vec P_2}$ એકબીજાથી $x$ અંતરે અને ${\vec P_1}$ || ${\vec P_2}$ છે.આ બંને ડાયપોલ વચ્ચે કેટલું બળ લાગતું હશે?View Solution
- 7બેટરીથી દૂર કરેલ એક કેપેસિટરનો કેપેસિટન્સ $C_o$ અને ઊર્જા $W_o$ અને છે.હવે ડાઇઇલેકિટ્રક અચલાંક $=$ $5$ ભરી દેતા નવોં કેપેસિટરનો કેપેસિટન્સ અને ઊર્જા કેટલી થાય?View Solution
- 8$20\, C$ નો એક વિદ્યુતભાર $2 \,cm$ અંતરે ગતિ કરે છે. થતું કાર્ય $2 \,J$ છે. તો બે બિંદુઓ વચ્ચેનો સ્થિતિમાનનો તફાવત ........$V$ છે.View Solution
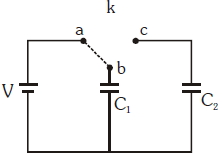
- 9નીચેના પરિપથમાં દર્શાવેલ બે સમાન કેપેસીટર $\mathrm{C}_{1}$ અને $\mathrm{C}_{2}$ નો કેપેસીટન્સ સમાન છે. જ્યારે કળ $k$ દ્વારા ટર્મિનલ $a$ અને $b$ ને જોડેલ હોય ત્યારે $\mathrm{C}_{1}$ કેપેસીટરને $ V\; volt \;emf $ ધરાવતી બેટરી વડે ચાર્જ કરવામાં આવે છે. હવે ટર્મિનલ $a$ અને $b$ ને અલગ કરી ટર્મિનલ $b$ અને $c$ જોડવામાં આવે તો કેટલા $\%$ ઉર્જાનો વ્યય થશે?View Solution
- 10$10^{-3}\;\mu C$ ના વિદ્યુતભારને $x - y$ યામપદ્ધતિના ઉગમબિંદુ પર મૂકેલો છે. બે બિદુઓ $A (\sqrt{2}, \sqrt{2})$ અને $B (2,0)$ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત ($V$ માં) કેટલો હશે?View Solution
