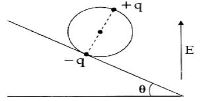
બે સમાન દળ $m$ અને વિરુદ્ધ વિજભાર $q$ ને $d$ અંતરે મૂકીને ડાયપોલ બનાવવામાં આવે છે.જેને એકસમાન વિદ્યુતક્ષેત્ર $E$ માં મુકેલ છે.જો તેને સંતુલન અવસ્થામાથી થોડુક ભ્રમણ કરવવામાં આવે તો તેની કોણીય આવૃતિ $\omega $ કેટલી થશે?
JEE MAIN 2019, Diffcult
b
Moment of inertia
Moment of inertia
\((I)=m\left(\frac{d}{2}\right)^{2} \times 2=\frac{m d^{2}}{2}\)
Now by \(\tau=1 \alpha\)
\((q E)(d \sin \theta)=\frac{m d^{2}}{2} \cdot \alpha\)
\(\alpha=\left(\frac{2 \mathrm{qE}}{\mathrm{md}}\right) \sin \theta\) for small \(\theta\)
\({\Rightarrow \alpha=\left(\frac{2 \mathrm{qE}}{\mathrm{md}}\right) \theta}\)
\(\Rightarrow \) Angular frequency \(\omega = \sqrt {\frac{{2qE}}{{md}}} \)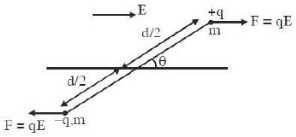
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
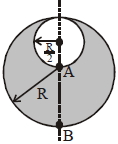
- 1$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.View Solution
- 2બે સમાન અને $-q$ ઋણ વિદ્યુતભારીત વિદ્યુતભારોને $Y$ અક્ષ પર $(0, a)$ અને $(0, -a)$ બિંદુ આગળ મૂકેલા છે એક ધન વિદ્યુતભાર $q$ સ્થિર સ્થિતિએ છે જે $(2a, 0)$ બિંદુથી ડાબી બાજુએ ગતિ કરે છે. આ વિદ્યુતભાર કયો હશે ?View Solution
- 3$4 \times 10^{-9} \;C\, m$ની ડાયપોલ ચાકમાત્રા ધરાવતી એક વિદ્યુત ડાયપોલ $5 \times 10^{4} \;N\,C ^{-1}$ નું માન ધરાવતાસમાનવિદ્યુતક્ષેત્ર સાથે $30^{\circ}$ નાકોણે રહેલી છે. આડાયપોલ પર લાગતાટોર્કનું માનશોધો.View Solution
- 4View Solutionમિલ્કનના તેલના બિંદુના પ્રયોગમાં બે પ્લેટ વચ્ચેના વિદ્યુતક્ષેત્રમાં સંતુલન સ્થિતિએ વિદ્યુતભારીત કણ મૂકેલ છે. જો પ્લેટો વચ્ચે વિદ્યુતક્ષેત્રની દિશા વિરૂદ્ધ હોય તો વિદ્યુતભારીત કણનો પ્રવેગ ગણો.
- 5એક તટસ્થ ગોળા પર $10^{12} \,\alpha$ - કણો પ્રતિ સેકન્ડ પડે છે. વિદ્યુતભાર પ્રસ્થાપિત તથા $2\ \mu C$ જેટલો વિદ્યુતભાર પ્રસ્થાપિત થવા માટે કેટલા ......$s$ નો સમય લાગશે?View Solution
- 6$+\sigma_{\mathrm{s}} \mathrm{C} / \mathrm{m}^2$ જેટલી નિયમિત પૃષ્ઠ વિદ્યુતભાર ધનતા ધરાવતી એક અનંત સમતલ તક્તિને $x-y$ સમતલમાં મૂકવામાં આવે છે. બીજા એક $+\lambda_{\mathrm{e}} \mathrm{C} / \mathrm{m}$ જેટલી નિયમિત રેખીય વિધુતભાર ધનતા ધરાવતા અનંત લંબાઈના લાંબા તાર ને $z=4 \mathrm{~m}$ સમતલ અને $y$-અક્ષને સમાંતર રાખવામાં આવે છે. જો મૂલ્યોમાં $\left|\sigma_s\right|=2\left|\lambda_{\mathrm{e}}\right|$ હોય તો $(0,0,2)$ સ્થાન આગળ તક્તિ ( પૃષ્ઠ) વિદ્યુતભાર અને રેખીય વિધુત ભાર ને કારણે મળતા વિધુતક્ષેત્રનાં મૂલ્યોનો ગુણોતર. . . . . છે.View Solution
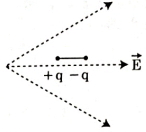
- 7View Solutionઆકૃતિમાં દર્શાવ્યા અનુસાર એક ડાયપોલને વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. તે કઈ દિશામાં ગતિ કરશે?
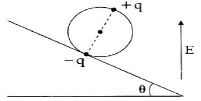
- 8$m $ દળના એક પૈડા પર વ્યાસના બે વિરુધ્ધ બિંદુઓ પર $+q$ અને $ -q$ વિદ્યુતભાર છે. એક ખરબચડા ઢળતા પાટિયા પર શિરોલંબ વિદ્યુતક્ષેત્ર $E$ ની હાજરીમાં તે સંતુલનમાં રહે છે. તો $E$ નું મૂલ્યView Solution
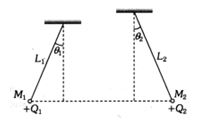
- 9$M_1$ અને $M_2$ દળ ધરાવતા બે નાના ગોળાઓને $L_1$ અને $L_2$ લંબાઇની વજન રહીત અવાહક દોરી વડે લટકાવેલ છે. ગોળાઓ પરનો વિદ્યુતભાર અનુક્રમે $Q_1$ અને $Q_2$ છે. ગોળાઓ એવી રીતે લટકાવેલ છે કે જેથી તેઓ સમક્ષીતીજ એક જ રેખામાં રહે તથા દોરીઓ શીરોલંબ સાથે આકૃતીમાં દર્શાવ્યા મુજબ $\theta_1$ અને $\theta_2$ માપનો ખૂણો બનાવે તો નીચેનામાંથી કઇ શરત $\theta_1$ $=$ $\theta_2$ થવા માટે જરૂરી છે.?View Solution
- 10$m $ દળના એક પૈડા પર વ્યાસના બે વિરુધ્ધ બિંદુઓ પર $+q$ અને $ -q$ વિદ્યુતભાર છે. એક ખરબચડા ઢળતા પાટિયા પર શિરોલંબ વિદ્યુતક્ષેત્ર $E$ ની હાજરીમાં તે સંતુલનમાં રહે છે. તો $E$ નું મૂલ્યView Solution