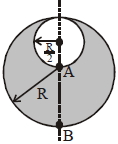
Fill the empty space with \(+\rho\) and \(-\rho\) charge density.
\(\left|\mathrm{E}_{\mathrm{A}}\right|=0+\frac{\operatorname{k\rho} \cdot \frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)^{3}}{\left(\frac{\mathrm{R}}{2}\right)^{2}}=\operatorname{k\rho} \frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)\)
\(\left|\mathrm{E}_{\mathrm{B}}\right|=\frac{\mathrm{k} \rho \cdot \frac{4}{3} \pi \mathrm{R}^{3}}{\mathrm{R}^{2}}-\frac{\mathrm{k} \rho \cdot \frac{4}{3} \pi\left(\frac{\mathrm{R}}{2}\right)^{3}}{\left(\frac{3 \mathrm{R}}{2}\right)^{2}}\)
\(=\operatorname{k\rho} \frac{4}{3} \pi \mathrm{R}-\mathrm{k} \rho \frac{4}{3} \pi \frac{\mathrm{R}}{18}=\mathrm{k} \rho \cdot \frac{4}{3} \pi\left(\frac{17 \mathrm{R}}{18}\right)\)
\(\frac{E_{A}}{E_{B}}=\frac{9}{17}=\frac{18}{34}\)
Download our appand get started for free
Similar Questions
- 1ઉગમબિંદુ પર કેન્દ્ર રહે તેમ વિધુતડાઇપોલ $x$-અક્ષ પર મુકેલ છે. $OP$ રેખા $x$-અક્ષ સાથે $\frac{\pi }{3}$ખૂણો બનાવે છે.જો $P$ બિદું આગળ વિધુતક્ષેત્ર $x$-અક્ષ સાથે બનાવેલ ખૂણો $\theta$ હોય તો $\theta$=______View Solution
- 2એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?View Solution
- 3આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.View Solution
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
- 4$Z$ પરમાણું ક્રમાંક ધરાવતા પરમાણુને $R$ ત્રીજ્યાના ગોળાની અંદર એકસમાન વિતરીત ઋણ વિદ્યુતભારના વિતરણ વડે ઘેરાયેલો અને કેન્દ્ર પાસે ઘન વિદ્યુતભાર ધરાવે છે તેમ ધ્યાનમાં લો. પરમાણુની અંદર કેન્દ્રથી $r$ અંતરે આવેલા બિંદુુએ વિદ્યુતક્ષેત્ર કેટલું છે?View Solution
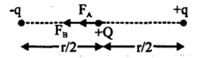
- 5આપેલ આકૃતિમાં $'O'$ એ $AB$ નું મધ્યબિંદુ હોય તો $Q$ વિદ્યુતભાર પરનું બળ ગણો.View Solution
- 6$\vec E\,\, = \,\,3\,\, \times \,\,{10^3}\,\hat i\,\,(N\,/\,\,C)$ લો. $10\, cm$ ની બાજુવાળા ચોરસમાંથી પસાર થતું ફલક્સ કેટલા .......$Nm^2/C$ હશે ? તેનો સ્પર્શક $X$ અક્ષ સાથે $60^°$ ખૂણો બનાવે છે.View Solution
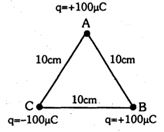
- 7આપેલ આકૃતિમાં $10\ cm$ ની બાજુઓ વાળા સમબાજુ ત્રિકોણની ખૂણાઓ ત્રણ બિંદુવત વિદ્યુતભારો આવેલા છે. $B$ આગળના વિદ્યુતભાર પર લાગતું પરિણામી બળ .....હશે.View Solution
- 8$R$ ત્રિજ્યા ધરાવતી રીંગ પર ધન વિદ્યુતભાર $Q$ વિતરિત થયેલ છે. $m$ દળ અને $-q$ વિદ્યુતભાર ધરાવતાં બિંદુવત કણને રીંગનાં અક્ષ પર કેન્દ્રથી $x$ અંતરે મુકેલ છે. જો તેને ત્યથી મુક્ત કરવામાં આવે અને $x < R$ હોય તો તેની સરળ આવર્તગતિનો આવર્તકાળ કેટલો થાય?View Solution
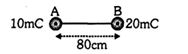
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે બિંદુ $A$ થી કેટલા...... $cm$ અંતરે વિદ્યુતક્ષેત્ર શૂન્ય હશે.View Solution
- 10અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
