બે સમાન ગોળાઓ $A$ અને $B$ને જ્યારે હવામાં ચોક્કસ અંતરે રાખવામાં આવે છે ત્યારે તે $F$ જેટલાં બળથી એકબીજાને અપાકર્ષે છે. ત્રીજો સમાન અવિદ્યુતભારીત ગોળો $C$ પ્રથમ ગોળા $A$ના અને ત્યારબાદ ગોળા $B$ના સંપર્કમાં લાવવામાં આવે છે. છેલ્લે તેને ગોળાઓ $A$ અને $B$ ના મધ્યબિંદુ પર મૂકવામાં આવે છે. ગોળા $C$ પર લાગતું બળ $...........$ હશે.
JEE MAIN 2022, Medium
b
Let \(q _{ A }= q _{ B }= q\)
Let \(q _{ A }= q _{ B }= q\)
When \(C\) is placed in contact with \(A\), charge on \(A\) and \( C\) will be \(=\frac{ q }{2}\)
Now \(C\) is placed in contact with \(B\), charge on \(B\) and \(C\) will be \(=\frac{q+\frac{q}{2}}{2}=\frac{3 q}{4}\)
\(F ^{\prime}= F _{2}- F _{1}=\frac{\left( K \frac{3 q }{4}- K \frac{ q }{2}\right)}{\frac{ r ^{2}}{4}} \cdot \frac{3 q }{4}\)
\(=\frac{3 Kq ^{2}}{4 r ^{2}}=\frac{3 F }{4}\)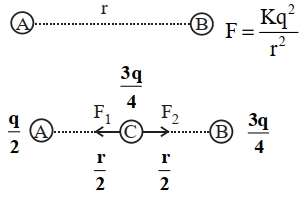
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બંધ સપાટીમાંથી બહાર આવતી વિદ્યુત બળરેખાઓની સંખ્યા $1000$ છે. તો સપાટી વડે ઘેરાતો વિદ્યુતભાર ............. $C$ છે.View Solution
- 2એક વિદ્યુત ડાઇપોલ $2 \times 10^5\ N/C$ ના સમાન વિદ્યુતક્ષેત્રમાં, ક્ષેત્ર સાથે $30^o $ ના કોણે રહેલો છે.આ સ્થિતિમાં તે $ 4\ Nm $ જેટલું ટોર્ક અનુભવે છે.જો ડાઇપોલની લંબાઇ $2\ cm $ હોય,તો ડાઇપોલ પરનો વિદ્યુતભાર કેટલો હશે?View Solution
- 3બંધ પૃષ્ઠની અંદરની બાજુએ $20\ \mu C$ નો વિદ્યુતભાર મૂકવામાં આવે તો પૃષ્ઠ સાથે સંકળાયેલ ફલક્સ છે. જો $\, 80\ \mu C$ બંને વિદ્યુતભાર પૃષ્ઠની અંદરની બાજુએ ઉમેરવામાં આવે તો ફલક્સમાં થતો ફેરફાર....... છે.View Solution
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે સમાન ગતિ ઉર્જા ધરાવતા પ્રોટોન અને $\alpha$ કણ ને એકરૂપ લંબ વિદ્યુતક્ષેત્રમાં પ્રક્ષેપિત કરવામાં આવ્યા છે, તોView Solution
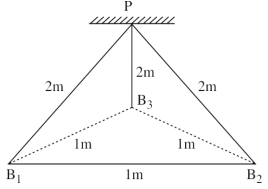
- 5ત્રણ દરેક $2 \,C$ જેટલા વિદ્યુતભારીત બોલને $2 \,m$ લંબાઈના સ્લિકના દોરાથી (આકૃતિમાં દર્શાવ્યા અનુસાર) સમાન બિંદુ $P$ આગળથી લટકાવવામાં આવ્યા છે. તેઓ $1 \,m$ બાજુનો સમબાજુ ત્રિકોણ બનાવે છે. વિદ્યુતભારીત બોલ પર લાગતુ કુલ બળ અને કોઇપણ બે વિદ્યુતભારો વચ્યે પ્રવર્તતા બળોનો ગુણોત્તર .......... થશે.View Solution
- 6સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
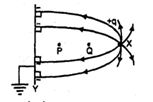
- 7પૃથ્વી સાથે જોડેલ ધાતુની તકતીની પાછળ એક બિંદુવત વિદ્યુતભાર મૂકેલો છે. આકૃતિમાં બતાવ્યા પ્રમાણે $P$ અને $Q$ બિંદુએ $X$ અને $Y$ ની વચ્ચે આવેલા છે. $P$ અને $Q$ આગળ વિદ્યુત ક્ષેત્રની $E_P$ અને $E_Q$ છે. નીચે આપેલ પૈકી કયું વિધાન સાચું છે ?View Solution
- 8$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.?View Solution
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ ધરાવતા ગોળીય કવચની અંદર $R$ ત્રિજયા અને $q$ વિદ્યુતભાર ધરાવતો ધાતુનો ગોળો છે. તો વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ વિરુદ્ધ તેના કેન્દ્ર $O$ થી અંતર $r$ સાથેનો ગ્રાફ લગભગ કેવો મળશે?View Solution
- 10View Solutionન્યુક્લિયસમાં પ્રોટોન અને પ્રોટોન વચ્ચે બળ ....... છે.
