આકૃતિ પરથી ગોળાની સમતોલન સ્થિતિમાં ,
\(F = \,\frac{{k{q^2}}}{{{r^2}}} = T\,\sin {15^ \circ }\,\,\,\,....(1)\,\,\,\)
\(\therefore \,\,\,mg\, = \,T\,\cos \,{15^ \circ }\,\,....(2)\)
પરિણામ \({\text{(1)}}\) અને \({\text{(2)}}\) નો ગુણોતર લેતા \(\therefore \,\frac{{k{q^2}}}{{mg{r^2}}}\, = \tan \,{15^ \circ }\,\,....(3)\,\,\,\,\therefore \,m'\, = \,m\, - \frac{m}{g}\,\)
પ્રવાહીમાં ગોળાનું અસરકારક વજન \(, mg'\, = \,mg\, - \,\frac{{0.8\,mg}}{{1.6}}\, = \frac{{mg}}{2}\,\)
પ્રવાહીમાં ગોળાઓ વચ્ચે લાગતું અપાકર્ષણ બળ \(F'\, = \frac{F}{K}\, = \frac{{k{q^2}}}{{K{r^2}}}\,\,\tan \,{15^ \circ }\, = \frac{{k{q^2}}}{{K{r^2}}}\,....(4)\)
પ્રવાહીમાં દોરીમાં તણાવબળ \(T'\,\cos \,{15^ \circ }\, = \frac{{mg}}{2}\,\,....(5)\,\,\therefore \,\tan \,{15^{ \circ \,}} = \frac{{2k{q^2}}}{{K\,mg\,{r^2}}}\,...(6)\,\)
પરિણામ \({\text{(3)}}\) અને \({\text{(6)}}\) પરથી \(\frac{{2k{q^2}}}{{K\,mg\,{r^2}}}\, = \frac{{k{q^2}}}{{mg{r^2}}}\,\,\therefore \,K = 2\)
OR
\({ \in _r}\,\, = \,\,\frac{{{d_b}}}{{{d_b}\,\, - \,\,{d_\ell }}}\,\, = \,\,\frac{{1.6}}{{1.6\,\, - \,\,0.8}}\,\, = \,\,2\)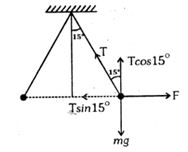
Download our appand get started for free
Similar Questions
- 1$a$ બાજુવાળા સમબાજુ ત્રિકોણના શિરોબંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે.તો એક વિદ્યુતભાર પર લાગતું બળ કેટલું થાય? $\left( {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right)$View Solution
- 2$Z$ પરમાણું ક્રમાંક ધરાવતા પરમાણુને $R$ ત્રીજ્યાના ગોળાની અંદર એકસમાન વિતરીત ઋણ વિદ્યુતભારના વિતરણ વડે ઘેરાયેલો અને કેન્દ્ર પાસે ઘન વિદ્યુતભાર ધરાવે છે તેમ ધ્યાનમાં લો. પરમાણુની અંદર કેન્દ્રથી $r$ અંતરે આવેલા બિંદુુએ વિદ્યુતક્ષેત્ર કેટલું છે?View Solution
- 3View Solutionમુક્ત અવકાશમાં વિદ્યુત પરમિટિવિટિ નું મૂલ્ય ........ છે.
- 4$1.2 \times 10^{-30} \,Cm$ અને $2.4 \times 10^{-30} \,Cm$ દ્વિ-ધ્રુવી ચાકમાત્રા ધરાવતી બે વિદ્યુત દ્વિ-ધ્રુવીઓને અનુક્રમે બે $5 \times 10^{4}$ $NC ^{-1}$ અને $15 \times 10^{4} \,NC ^{-1}$ જેટલા નિયમીત વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. વિદ્યુત દ્વિ-ધુવીઓ દ્વારા અનુભવતા મહત્તમ ટોર્કનો ગુણોત્તર $\frac{1}{x}$ છે. $x$ નું મૂલ્ય ......... થશે.View Solution
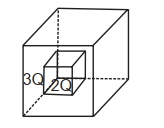
- 5આકૃતિતિાં દર્શાવ્યા અનુસાર $2 Q$ અને $3 Q$ જેટલો વિદ્યુતભાર ઘેરતા બે પોલા સમકેન્દ્રીય સમઘનો $C_1$ અને $C_2$ છે. $C_1$ અને $\mathrm{C}_2$ માંથી પસાર થતા વિદ્યુત ફ્લક્સનો ગુણોત્તર_____________છે.View Solution
- 6$\varepsilon$$_r$ નું પારિમાણિક સૂત્ર.......View Solution
- 7વિદ્યુતક્ષેત્ર શોધવા ગાઉસનો નિયમ $|\overrightarrow{\mathrm{E}}|=\frac{q_{\mathrm{enc}}}{\varepsilon_{0}|\mathrm{A}|}$ વાપરવામાં આવે છે.જ્યાં $\varepsilon_{0}$ શૂન્યાવકાશની પરમિટિવિટી, $A$ ગાઉસીયન સપાટીનું ક્ષેત્રફળ અને $q_{enc}$ એ ગાઉસીયન સપાટીની અંદર રહેલ વિજભાર છે.ઉપરનું સૂત્ર ક્યારે વાપરવામાં આવે છે?View Solution
- 8એક બિંદુવત વીજભાર $q_1=4{q_0}$ ઉગમબિંદુ પર રાખેલ છે. બીજો બિંદુવત વીજભાર $q _2=- q _0,\;\; x=12\,cm$ પર રહેલ છે. પ્રોટોનનો વીજભાર $q_0$ છે પ્રોટોનને $x$ અક્ષ પર એવી રીતે રાખવામાં આવે છે કે જેથી પ્રોટોન પર સ્થિત વિદ્યુતબળ શૂન્ય છે. આ પરિસ્થિતિમાં, ઉગમબિંદુથી પ્રોટોનનું સ્થાન $............cm$ છે.View Solution
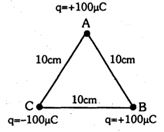
- 9આપેલ આકૃતિમાં $10\ cm$ ની બાજુઓ વાળા સમબાજુ ત્રિકોણની ખૂણાઓ ત્રણ બિંદુવત વિદ્યુતભારો આવેલા છે. $B$ આગળના વિદ્યુતભાર પર લાગતું પરિણામી બળ .....હશે.View Solution
- 10$q$ વિદ્યુતભાર ધરાવતા બે ધન આયનો વચ્ચેનું અંતર $d $ છે. જો તેમની વચ્ચેનું અપાકર્ષણ બળ $F $ હોય, તો દરેક આયન પર ખૂટતાં ઇલેકટ્રોનની સંખ્યા કેટલી હશે? ($e$ ઇલેક્ટ્રોન પરનો વિદ્યુતભાર છે)View Solution
