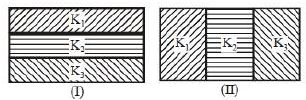
\(C_{1}=\frac{3 \varepsilon_{0} A K_{1}}{d}\)
\(C_{2}=\frac{3 \varepsilon_{0} A K_{2}}{d}\)
\(C_{3}=\frac{3 \varepsilon_{0} A K_{3}}{d}\)
\(\frac{1}{C_{e q}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\)
\(\Rightarrow \quad C_{e q}=\frac{3 \varepsilon_{0} A K_{1} K_{2} K_{3}}{d\left(K_{1} K_{2}+K_{2} K_{3}+K_{3} K_{1}\right)}.........(i)\)
\(C_{1}=\frac{\varepsilon_{0} K_{1} A}{3 d}\)
\(C_{2}=\frac{\varepsilon_{0} K_{2} A}{3 d}\)
\(C_{3}=\frac{\varepsilon_{0} K_{3} A}{3 d}\)
\(C_{e q}^{\prime} =C_{1}+C_{2}+C_{3} \)
\( = \frac{{{\varepsilon _0}A}}{{3d}}({K_1} + {K_2} + {K_3}).........(ii)\)
Now,
\(\frac{{{E_1}}}{{{E_2}}} = \frac{{\frac{1}{2}{C_{eq}} \cdot {V^2}}}{{\frac{1}{2}C_{eq}^\prime {V^2}}} = \frac{{9{K_1}{K_2}{K_3}}}{{\left( {{K_1} + {K_2} + {K_3}} \right)\left( {{K_1}{K_2} + {K_2}{K_3} + {K_3}{K_1}} \right)}}\)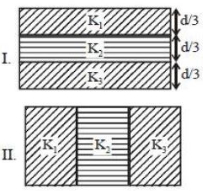
Download our appand get started for free
Similar Questions
- 1$100\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $E$ છે. $60\, W$ બલ્બથી $3\;m$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા $\sqrt{\frac{x}{5}} E$ હોય તો તો $x$નું મૂલ્ય કેટલું હશે?View Solution
- 2View Solutionવિદ્યુતભારિત પોલા વાહક ગોળાની અંદરની બાજુએ સ્થિતિમાન ...... છે.
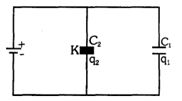
- 3આપેલ રેખાચિત્રમાં બે સમાન કેપેસિટર $C_1$ અને $C_2$ ને બેટરી સાથે જોડેલ છે. $C_1$ ની પ્લેટો વચ્ચે હવા વડે ભરવામાં આવે છે. અને $C_2$ વચ્ચેની પ્લેટો વચ્ચે અવાહક દ્રવ્યને ભરવામાંં આવે છે, તો,View Solution
- 4$5\,mm$ અને $10\,mm$ ત્રિજ્યાઓ ધરાવતા અને નિયમિત વિદ્યુતભારીત બે નળાકારીય સુવાહકો $A$ અને $B$ ને $2\,cm$ અંતરે છૂટા પાડેલા છે. જો ગોળાઓને એક સુવાહક તાર વડે જોડવામાં આવે તો, સંતુલન અવસ્થામાં ગોળા $A$ અને $B$ ની સપાટી ઉપર વિદ્યુતક્ષેત્રનાં :મૂલ્યોનો ગુણોત્તર $.......$ થશે.View Solution
- 5View Solutionપુરો વિદ્યુતભાર થયેલા એક સમાંતર પ્લેટવાળા કેેેસીટરને બેટરી સાથે જોડેલ રાખીને અવાહક સાધનો વડે તેની પ્લેટોને એકબીજાથી દૂર કરવામાં આવે છે. આ સ્થિતિમાં નીચેનામાંથી કઈ રાશિનું મૂલ્ય ઘટશે?
- 6બેટરીથી દૂર કરેલ એક કેપેસિટરનો કેપેસિટન્સ $C_o$ અને ઊર્જા $W_o$ અને છે.હવે ડાઇઇલેકિટ્રક અચલાંક $=$ $5$ ભરી દેતા નવોં કેપેસિટરનો કેપેસિટન્સ અને ઊર્જા કેટલી થાય?View Solution
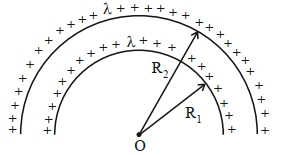
- 7સમાન રેખીય વીજભાર ધનતા $\lambda$ ધરાવતી $R _1$ અને $R _2$ ત્રિજયાની સમકેન્દ્રિય અર્ધલયોના કેન્દ્ર સ્થાને વિદ્યુત સ્થિતિમાન $.............$ છે.View Solution
- 8બે પ્લેટો એકબીજાથી $20\, cm$ દૂર છે. તેમની વચ્ચે વિદ્યુુત સ્થિતિમાનનો તફાવત $10\, volt$ છે, તો બે પ્લેટો વચ્ચે વિદ્યુતક્ષેત્ર ......$Vm^{-1}$View Solution
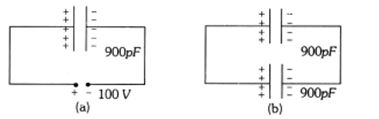
- 9આકૃતીમાં દર્શાવેલ કેપેસીટરમાં સંગ્રહીત ઉર્જા $4.5 \times 10^{-6}\ J$ છે. જો બેટરીને બીજા $900\,pF$ ના કેપેસીટર વડે બદલવામાં આવે તો તંત્રની કુલ ઉર્જા શોધો ?View Solution
- 10$10\,m$ ત્રિજયા ધરાવતા વર્તુળના કેન્દ્ર પર $10$ યુનિટ વિદ્યુતભાર મૂકેલો છે. તો $1$ એકમ વિદ્યુતભારને વર્તુળના પરિઘ પર પરિભ્રમણ કરાવવા માટે ....... એકમ કાર્ય કરવું પડેView Solution
