બે સમાંતર તાર ${i_1}$ અને ${i_2}$ વિધુતપ્રવાહનું વહન કરે છે. (${i_1} > {i_2}$ ) જયારે પ્રવાહ એક જ દિશામાં હોય ત્યારે તારની મઘ્યમાં આવેલ બિંદુએ ચુંબકીયક્ષેત્ર $10\, \mu T. $ છે.જયારે ${i_2}$ ની દિશા ઉલટાવવામાં આવે ત્યારે તે બિંદુ આગળ ચુંબકીયક્ષેત્ર $30\, \mu T.$ થાય તો $\frac{i_1}{i_2}$ કેટલું થાય?
Diffcult
Download our app for free and get started
c
\({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_1}}}{x} \otimes \) \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_2}}}{x}\)
\({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_1}}}{x} \otimes \) \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_2}}}{x}\)
\({B_{net}} = \frac{{{\mu _0}}}{{4\pi }} \times \frac{2}{x}({i_1} - {i_2})\)
\(⇒\) \(10 \times {10^{ - 6}} = \frac{{{\mu _0}}}{{4\pi }}.\frac{2}{x}({i_1} - {i_2})\) \(.....(i) \)
\({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_1}}}{x} \otimes \) \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_2}}}{x} \otimes \)
\({B_{net}} = \frac{{{\mu _0}}}{{4\pi }}.\frac{2}{x}({i_1} + {i_2})\)
\(⇒\) \(30 \times {10^{ - 6}} = \frac{{{\mu _0}}}{{4\pi }}.\frac{2}{x}({i_1} + {i_2})\) \(......(ii)\)
\(\frac{{{i_1} + {i_2}}}{{{i_1} - {i_2}}} = \frac{3}{1}\) \(⇒\) \(\frac{{{i_1}}}{{{i_2}}} = \frac{2}{1}\) 
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
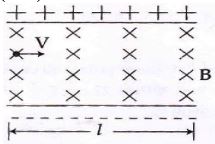
- 1એક ચલિત ગૂંચળું ધરાવતા ગેલ્વેનોમીટરમાં $100$ આંટા અને દરેક આંટાને $2.0 \mathrm{~cm}^2$ નું ક્ષેત્રફળ છે. ચુંબક દ્વારા ઉત્પન્ન ચુંબકીય ક્ષેત્ર $0.01 \mathrm{~T}$છે અને જ્યારે તેમાંથી $10 \mathrm{~mA}$ પ્રવાહ પસાર થાય છે ત્યારે ગૂંચળાનું કોણાવર્તન $0.05$ $radian$ મળે છે. ગેલ્વેનોમીટરમાં લટકાવેલ તાર માટે બળ અચળાંક $x \times 10^{-5} \mathrm{~N}-\mathrm{m} / \mathrm{rad}$ છે. $x$ નું મૂલ્ય__________છે.View Solution
- 2$100$ વોલ્ટ વોલ્ટમીટર જેનો અવરોધ $20\ k\Omega$ છે. તેને ખૂબ ઉંચા અવરોધ $R$ સાથે શ્રેણીમાં જોડવામાં આવે છે જ્યારે તેને $110$ વોલ્ટની લાઈન સાથે જોડેલ હોય ત્યારે તે $5$ વોલ્ટ નોંધે છે. તો $R$ નું મુલ્ય કેટલું છે ?View Solution
- 3$l$ લંબાઈના સાદા લોલકમાં એક છેડે લોખંડનો ગોળો લટકાવેલો છે.આ લોલક $d.c.$ પ્રવાહ ધરાવતા સમક્ષિતિજ ગૂચળાની ઉપર દોલનો કરે છે તો લોલકનો આવર્તકાળ $T$ ......View Solution
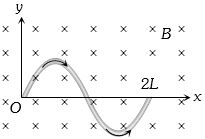
- 4$ y = a\sin \,\left( {\frac{{\pi x}}{L}} \right)\,0 \le x \le 2L. $ ના આકારમાં તારને વાળતા તેના પર કેટલું બળ લાગશે?View Solution
- 5એક વીજભાર યુક્ત કણ યુંબકીયક્ષેત્ર $B$ માં ગતિ કરે છે, તેના વેગના ધટકો $B$ પર છે અને $B$ ને લંબ છે. વીજભારયુક્ત કણનો માર્ગ કેવો હશે?View Solution
- 6$10 \mathrm{~cm}$ ત્રિજ્યા ધરાવતી અને સજ્જઙ રીતે વીંટાળેલ $100$ આાંટાના ગૂંચળામાંથી $7$ $A$નો પ્રવાહ પસાર થાય છે. ગૂંચળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્રનું મૂલ્ય. . . . . . . . . . હશે.View Solution
[મુક્તાવકાશ માટે પારગમ્યતા $4 \pi \times 10^{-7}$ $SI$ એકમ લો]
- 7'$a$' ત્રિજ્યાના એક સુરેખ વાહક તાર સ્થિર પ્રવાહ $I$ નું વહન કરે છે. આ પ્રવાહ્ સમગ્ર આડછેદ પર વિતરીત થયેલ છે. તારની અક્ષથી $\frac{a}{2}$ અને $2 \mathrm{a}$ અંતર આગળના ચુંબકીય ક્ષેત્રનો ગુણોતર . . . . .છે.View Solution
- 8$f $ આવૃત્તિવાળું વિદ્યુતક્ષેત્ર $R$ ત્રિજયાની સાઇકલોટ્રોનની ડીશ પર લગાવવામાં આવે છે.સાઇકલોટ્રોનમાં ચુંબકીયક્ષેત્ર $B$ અને પ્રોટ્રોનની ગતિઊર્જા $K$View Solution
પ્રોટોનને(દળ = $m$) પ્રવેગિત કરવા સાયક્લોટ્રોનની ડિસ (ત્રિજ્યા $R$) ની વચ્ચે $f$ આવૃતિ ધરાવતું પ્રત્યાવર્તી વિદ્યુતક્ષેત્ર લગાવવામાં આવે છે. સાયક્લોટ્રોનમાં વપરાતું ચુંબકીય ક્ષેત્ર $(B)$ અને પ્રોટોન બીમના કારણે ઉત્પન્ન થતી ગતિઊર્જા $(K)$ શેના વડે આપી શકાય?
- 9ગેલ્વેનોમીટરના કોઇલનો અવરોઘ $100\,\Omega$ છે અને તે $30\,mA $ ના પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન દર્શાવે છે.તેને $30 \,V $ માપીશકે તેવા વોલ્ટમીટર તરીકે કાર્ય કરવવા કેટલો અવરોધ($\Omega$) જોડાવો પડે?View Solution
- 10સમાન વિદ્યુતઘનતા $\sigma $ ધરાવતા એક વીજભારીત સમાંતર પ્લેટ્સ કેપેસિટરની અંદર એક ઇલેકટ્રોન સીધો ગતિ કરે છે,પ્લેટ્સ વચ્ચેની જગ્યા આકૃતિમાં બતાવ્યા મુજબ $B $ તીવ્રતાનું સમાન ચુંબકીયક્ષેત્રથી ભરવામાં આવેલ છે.ગુરુત્વાકર્ષણની અસર અવગણતા, કેપેસિટરમાં આ ઇલેકટ્રોનની સુરેખ પંથ પર ગતિનો સમય કેટલો હશે?View Solution
