બે સમકેન્દ્રિય ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે, ${R_1}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_1}$ અને ${R_2}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_2}$ છે,તો કેન્દ્રથી $x$ અંતરે આવેલા બિંદુએ વોલ્ટેજ કેટલો થાય? (${R_2} > x > {R_1}$)
Diffcult
Download our app for free and get started
b
\({V_1} = \frac{{{Q_1}}}{{{R_1}}} + \frac{{{Q_2}}}{{{R_2}}}\)…….. \((i)\)
\({V_1} = \frac{{{Q_1}}}{{{R_1}}} + \frac{{{Q_2}}}{{{R_2}}}\)…….. \((i)\)
\({V_2} = \frac{{{Q_2}}}{{{R_2}}} + \frac{{{Q_1}}}{{{R_2}}}\)…….. \((ii)\)
\(V = \frac{{{Q_1}}}{x} + \frac{{{Q_2}}}{{{R_2}}} = \frac{{{Q_1}}}{x} + {V_1} - \frac{{{Q_1}}}{{{R_1}}}\) \( = {Q_1}\left( {\frac{1}{x} - \frac{1}{{{R_1}}}} \right) + {V_1} = \frac{{{Q_1}({R_1} - x)}}{{x{R_1}}} + {V_1}\) ……..\((iii)\)
\({V_1} - {V_2} = \frac{{{Q_1}}}{{{R_1}}} - \frac{{{Q_2}}}{{{R_2}}}\)
\(==>\) \(({V_1} - {V_2}){R_1}{R_2} = {R_2}{Q_1} - {R_1}{Q_1}\)
\(==>\) \({Q_1} = \frac{{({V_1} - {V_2}){R_1}{R_2}}}{{{R_2} - {R_1}}}\) \(V = \frac{{({R_1} - x)\,({V_1} - {V_2}){R_1}{R_2}}}{{x{R_1}({R_2} - {R_1})}} + {V_1}\)
\(==>\) \(V = \frac{{{V_1}{R_1}({R_2} - x) + {V_2}{R_2}(x - {R_1})}}{{x({R_2} - {R_1})}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
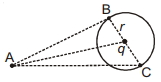
- 1$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 2હવામાં ગોળાકારની કેપેસિટિ $50 \,\mu F$ છે. અને તેને તેલમાં ડૂબડતાં તે બને $110 \,\mu F$ છે. તો તેલનો ડાઈ ઈલેકટ્રીક ગણો.View Solution
- 3$1\,m$ ત્રિજ્યા ધરાવતા વાહક ગોળાનું કેપેસીટન્સ કેટલું થાય?View Solution
- 4બે ગોળાકાર તકતીઓને $5$ $mm $ અંતરે રાખી તેમની વચ્ચે $2.2$ ડાયઇલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકો.એક સમાંતર પ્લેટ કેપેસિટરર્સ બનાવવામાં આવે છે.જયારે અવાહકનું વિદ્યુતક્ષેત્ર $3 \times 10^4$ $ Vm^{-1}$ હોય,ત્યારે ધન પ્લેટ (તકતી) ની વિદ્યુતભાર ઘનતા લગભગ _______ હશે.View Solution
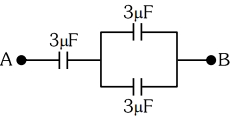
- 5નીચેના પરિપથમાં દર્શાવેલા સંઘારકના તંત્રની સમતુલ્ય સંઘારકતા $...........\mu F$ છે.View Solution
- 6વિદ્યુતભારીત ધાતુ માટે નીચેના પૈકી કયુ વિધાન હંમેશા સાચું હોય છે?View Solution
$(1)$ પૃષ્ઠની બહારની બાજુએ વિદ્યુતક્ષેત્ર એ પૃષ્ઠને સમાંતર હશે.
$(2) \,E_{in} = 0\,\,$
$ (3)$ વિદ્યુત ક્ષેત્ર રેખાઓ સમસ્થિતિમાન પૃષ્ઠને લંબ હોય છે.
- 7ઉગમબિંદુથી $R_o$ અંતરે એક સમાન ગોલીય સંમિતિ ધરાવતી પૃષ્ઠ વિધુતભાર ઘનતા રહેલ છે. વિદ્યુતભાર વિતરણ પ્રારંભમાં સ્થિર છે, અને પછી તેનું પરસ્પર અપાકર્ષણ થવાને કરાણે સમાન રીતે વિસ્તરણ થાય છે. વિસ્તરણ માટે તેની તત્ક્ષણિક ત્રિજ્યા $R(t)$ ના વિધેય તરીકે ઝડપ $V(R(t))$ ને રજુ કરતી આકૃતિ નીચેનામાથી કઈ છે.View Solution
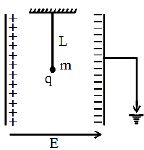
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે $L$ લંબાઈ ધરાવતા લોલકને $E$ વિદ્યુતક્ષેત્ર ધરાવતા સમાંતર પ્લેટ કેપેસીટર વચ્ચે મૂકેલું છે.તેનું દળ $m$ અને વિદ્યુતભાર $q$ હોય તો લોલકનો આવર્તકાળ કેટલો થશે?View Solution
- 9બે અલગ કરેલા વાહકોને એક વાહકમાંથી બીજા વાહકમાં ઈલેકટ્રોન પસાર કરી ચાર્જ કરેલ છે. એક વાહકમાંથી બીજા વાહકમાં $6.25 \times 10^{15}$ ઈલેકટ્રોન પસાર કરતા $100\, V$ નો વિદ્યુત સ્થિતિમાન ઉત્પન્ન થાય તો તંત્રની કેપેસિટિ કેટલા ........$\mu F$ હશે ?View Solution
- 10જો $y -$ અક્ષ પર $y=-a$ પર $y=+a$ પર બે એક સરખાં ધન ચાર્જ મુકવામાં આવે છે. આ સ્થિતિમાં $x$ અક્ષ પર સ્થિતિમાનનો આલેખ કેટલો મળશે ?View Solution