બે તાર $A$ અને $B$ ને સમાન બળથી ખેંચવામા આવે છે જો $A$ અને $B$ માટે $Y_A: Y_B=1: 2, r_A: r_B=3: 1$ અને $L_A: L_B=4: 1$ તો $\left(\frac{\Delta L_A}{\Delta L_B}\right)$ કેટલું હશે.
Medium
b
(b)
(b)
\(\Delta x=\frac{F L}{A Y}\)
For wire \(A\)
\(\Delta L_A=\frac{F \cdot L_A}{\pi r_A^2 \cdot Y_A} \ldots (1)\)
For wire \(B\)
\(\Delta L_B=\frac{F \cdot L_B}{\pi r_B^2 \cdot Y_B} \ldots (2)\)
Divide \((1)\) by \((2)\)
\(\frac{\Delta L_A}{\Delta L_B}=\frac{F \cdot L_A}{\pi r_A^2 \cdot Y_A} \times \frac{\pi r_B^2 \cdot Y_B}{F \times L_B}=\frac{L_A}{L_B} \times\left(\frac{r_B}{r_A}\right)^2 \times \frac{Y_B}{Y_A}\)
Substituting the value of ratio's
\(\frac{\Delta L_A}{\Delta L_B}=\frac{4}{1} \times\left(\frac{1}{3}\right)^2 \times \frac{2}{1}=\frac{8}{9}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસ્થિતિસ્થાપક સ્થિતિઊર્જા ઘનતા માટે નીચેનામાથી શું સાચું છે
- 2$R$ ત્રિજયાના કોપરના તારને તોડવા માટે $F$ બળની જરૂર પડે છે,તો $2R$ ત્રિજયાના કોપરના તારને તોડવા માટે કેટલા બળની જરૂર પડે?View Solution
- 3ઉપરના છેડે જડિત કરેળ તાર પર $F$ બળ લગાવીને લંબાઈ $l$ સુધી લંબાય છે. તો તારાને ખેંચવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 4બે માણસો તેઓની તરફ એક તારને ખેંચી રહ્યા છે. દરેક વ્યક્તિ તાર ઉપ૨ $200 \mathrm{~N}$ નું બળ લગાવે છે. તારના દ્રવ્યનો યંગ મોડયુલસ $1 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}$ છે. તારની મૂળ લંબાઈ $2 \mathrm{~m}$ છે અને આડછેદનું ક્ષેત્રફળ $2 \mathrm{~cm}^2$ છે. તારની લંબાઈ ...........$\mu \mathrm{m}$ વધશે.View Solution
- 5View Solutionહુકનો નિયમ શું વ્યાખ્યાયિત કરે છે ?
- 6$l$ લંબાઈ અને $m$ દળ ધરાવતો સળીયો ઉભી રેખામાં $M$ દળના પદાર્થ સાથે લટકેલ છે. તો તણાવ પ્રતીબળ અંતર $x$ તેના મુખ્ય ટેકાથી.... ($A \rightarrow$ સળીયાના આડછેદનું ક્ષેત્રફળ)View Solution
- 7View Solutionયંગ મોડ્યુલસ નો એકમ ?
- 8લાંબા પાતળા સ્ટીલના તાર પર $F$ જેટલું દબનીય બળ લગાવવામાં આવે છે. અને ગરમ કરવામાં આવે છે કે જેથી તેનું તાપમાન $\Delta T$ જેટલું વધે છે. તેની લંબાઈમાં કોઈ ફેરફાર થતો નથી. $l$ તારની લંબાઈ, $A$ આડછેડનું ક્ષેત્રફળ, $Y$ યંગ મોડ્યુલૂસ અને $\alpha $ રેખીય પ્રસરણાંક હોય તો $F$ નું મૂલ્ય કેટલું હશે?View Solution
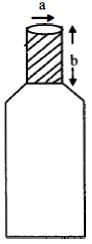
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે બોટલના ઉપરના ભાગની ત્રિજ્યા $a$ અને લંબાઈ $b$ છે. બીજા એક $\left( {a + \Delta a} \right)$ $\left( {\Delta a < < a} \right)$ ત્રિજ્યા ધરાવતા બુચને દબાવીને બોટલમાં ફિટ કરવામાં આવે છે. જો બૂચનો બલ્ક મોડ્યુલસ $B$ અને બોટલ અને બુચ વચ્ચેનો ઘર્ષણાંક $\mu $ હોય તો બુચને બોટલમાં ફિટ કરવા માટે કેટલા બળની જરૂર પડે?View Solution
- 10એક પટ્ટી જેના પર હળવી સ્પ્રિંગ દ્વારા થોડાક વજન લટકાવવામાં આવેલ છે. જ્યારે તંત્રમાં ખલેલ પહોચાડવામાં આવે ત્યારે તેનો આવર્તકાળ $0.6$ $s$ છે થોડુંક વજન વધારતા આ આવર્તકાળ $0.7$ $s$ થાય જાય છે વધારાના વજન દ્વારા લંબાઈમાં ...... $cm$ વધારો થશે.View Solution
