બે વીજભારો $5 Q$ અને $-2 Q$ અનુક્રમે બિંદુ $(3 a, 0)$ અને $(-5 a, 0)$ પર રહેલા છે. ઉગમબિંદુ પર કેન્દ્ર અને $4 a$ ત્રિજ્યાવાળા ગોળામાંથી પસાર થતું ફલકસ_______છે.
JEE MAIN 2024, Diffcult
b
\(5 \mathrm{Q}\) charge is inside the spherical region flux through sphere \(=\frac{5 \mathrm{Q}}{\varepsilon_0}\)
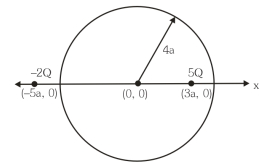
\(5 \mathrm{Q}\) charge is inside the spherical region flux through sphere \(=\frac{5 \mathrm{Q}}{\varepsilon_0}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\rho (r)\,\, = \,\,{\rho _0}\left( {\frac{5}{4}\, - \,\,\frac{r}{R}} \right)$ એ વિદ્યુતભારની ઘનતા સાથે બદલાતું ગોળીય સંમિત વિદ્યુતભારનું વિતરણ આપે છે. જે $r = R$, અને $\rho (r)\,\, = \,\,0$ માટે $r > R$ જ્યાં $r$ એ ઉગમબિંદુથી અંતર છે. ઉગમબિંદુથી $r$ અંતરે $(r < R)$ વિદ્યુતક્ષેત્ર ....... દ્વારા આપવામાં આવે છે.View Solution
- 2$+\sigma_{\mathrm{s}} \mathrm{C} / \mathrm{m}^2$ જેટલી નિયમિત પૃષ્ઠ વિદ્યુતભાર ધનતા ધરાવતી એક અનંત સમતલ તક્તિને $x-y$ સમતલમાં મૂકવામાં આવે છે. બીજા એક $+\lambda_{\mathrm{e}} \mathrm{C} / \mathrm{m}$ જેટલી નિયમિત રેખીય વિધુતભાર ધનતા ધરાવતા અનંત લંબાઈના લાંબા તાર ને $z=4 \mathrm{~m}$ સમતલ અને $y$-અક્ષને સમાંતર રાખવામાં આવે છે. જો મૂલ્યોમાં $\left|\sigma_s\right|=2\left|\lambda_{\mathrm{e}}\right|$ હોય તો $(0,0,2)$ સ્થાન આગળ તક્તિ ( પૃષ્ઠ) વિદ્યુતભાર અને રેખીય વિધુત ભાર ને કારણે મળતા વિધુતક્ષેત્રનાં મૂલ્યોનો ગુણોતર. . . . . છે.View Solution
- 3અવગણ્ય કદ ધરાવતાં બે એક સરખા વીજભારિત ગોળાઓ અનુક્રમે $2.1\, nC$ અને $-0.1\, nC$ વીજભાર ધરાવે છે. બંનેને એકબીજાનાં સંપર્કમાં લાવી $0.5$ મીટર અંતર માટે જુદા પાડવામાં આવે છે. બંને ગોળાઓ વચ્ચે ઉદ્દભવતું સ્થિત વિદ્યુત બળ $.......... \, \times 10^{-9} \,N$ છે. [ $4 \pi \varepsilon_{0}=\frac{1}{9 \times 10^{9}} SI$ એકમ આપેલ છે. ]View Solution
- 4અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
- 5$5\,\mu C$ બિંદુવત વિજભારથી $80\, cm$ અંતરે વિદ્યુતક્ષેત્રની પ્રબળતા કેટલી હશે?View Solution
- 6હવામાં $r$ અંતરે રહેલા બે વિદ્યુતભાર પર લાગતું બળ $F$ છે.હવે $k$ ડાઇઇલેકિટ્રક ધરાવતા માધ્યમ મૂકવાથી લાગતું બળ કેટલું થાય?View Solution
- 7$10\, mg$ દળ ધરાવતાં બે નાના ગોળાઓને $0.5\, m$ લંબાઈની દોરી દ્વારા એક બિંદુ પરથી લટકાવવામાં આવ્યા છે. બંને પર એક સરખો વિજભાર છે અને એકબીજાને $0.20\, m$ અંતર સુધી અપાકર્ષિત કરે છે. દરેક ગોળા પરનો વિજભાર $\frac{ a }{21} \times 10^{-8} \, C$ છે તો $a$ નું મૂલ્ય ........ હશે. [$g=10 \,ms ^{-2}$ આપેલ છે. ]View Solution
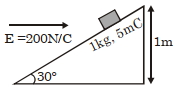
- 8આકૃતિમાં દર્શાવ્યા મુજબ $200 \, \frac{ N }{ C }$ સમાન સમક્ષિતીજ વિદ્યુત ક્ષેત્રમાં મૂકેલ ઢળતી સપાટી, સમક્ષિતીજ સાથે $30^{\circ}$ નો કોણ રચે છે. $1\, kg$ દળ અને $5\, mC$ વિજભાર ધરાવતા પદાર્થને આ ઢળતી સપાટી $1\, m$ ઊંચાઈ વિરામ સ્થાનેથી સરકવા દેવામાં આવે છે. જો ઘર્ષણાંક $0.2$ હોય તો તળીયે પહોંચવા માટે લીધેલો સમય શોધો.($s$ માં)View Solution
$\left[ g =9.8 \,m / s ^{2}, \sin 30^{\circ}=\frac{1}{2}\right.$; $\left.\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$
- 9$+ q$ વિદ્યુતભાર $L$ લંબાઈના સમઘનના કેન્દ્ર પર મૂકેલો છે, તો સમઘનમાંથી કેટલું ફ્લક્સ પસાર થાય?View Solution
- 10View Solutionમુક્ત અવકાશમાં વિદ્યુત પરમિટિવિટિ નું મૂલ્ય ........ છે.
