બેઇઝની પ્રબળતાનો ક્રમ કયો છે?
$\mathop {{H_3}C\mathop C\limits^ \ominus {H_2}}\limits_{(i)} \,,$$\mathop {{H_2}C = \mathop C\limits^ \ominus H}\limits_{(ii)} $ અને $\mathop {H - C \equiv \mathop C\limits^ \ominus }\limits_{(iii)} $
AIPMT 2008, Medium
Download our app for free and get started
b
Weaker the acid, strongest is its conjugate base.
Weaker the acid, strongest is its conjugate base.
Among alkane, alkene and alkyne are most acidic and alkanes are least acidic, so the order of base strengths
alkane \(>\) alkene \(>\) alkyne
\(C H_{3} \stackrel{\ominus}{C} H_{2}>H_{2} C=\stackrel{\ominus}{C} H>H-C \equiv {C}^{\ominus}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકોણ સૌથી વધુ સ્થિર છે ?
- 2View Solutionનીચેના પદાર્થો માટે વધતી એસિડિકતાનો સાચો ક્રમ કયો છે ?
- 3View Solutionનીચેનામાંથી કયો સૌથી સ્થિર કાર્બોકેટાયન છે ?
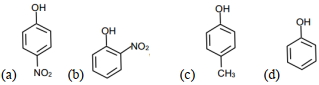
- 4View Solutionનીચેનામાંથી કયો સૌથી એસિડિક પદાર્થ છે ?
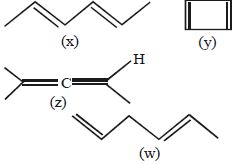
- 5View Solutionકયો પદાર્થ ન્યુનતમ હાઈડ્રોજીનેશન ઉષ્મા ધરાવે છે ?
- 6નીચેનાને તેમના $pK_a$ મૂલ્યોના વધતા ક્રમમાં ગોઠવોView Solution
$(x)\begin{array}{*{20}{c}}
{O\,\,\,}\\
{||\,\,\,}\\
{C{H_3} - S - O - H}\\
{||\,\,\,\,}\\
{O\,\,\,\,}
\end{array}$$\begin{array}{*{20}{c}}
{\,\,\,\,\,O}\\
{\,\,\,\,\,\,||}\\
{(y)\,\,\,C{H_3} - C - O - H}
\end{array}$$(z)\,\, CH_3 -OH$
- 7View Solutionએસિડિક સ્વભાવનો ક્રમ શું હશે ?
- 8નીચેના ઘટકો $(A)$, $(B)$,અને $(C)$ $(D)$માંથી કયા ઘટકો $sp^2$ સંકૃત કાર્બન ધરાવે છે ?$CH_3^ + \,,\,\,\,CH_3^ - \,\,,\,\,\mathop C\limits^ \bullet {H_3}\,,\,\,C{H_2}$View Solution
- 9નીચેના કાર્બોકેટાયનની સ્થાયિતામાં ઘટાડો થવાનો સાચો ક્રમ કયો છેView Solution
$\mathop {C{H_3} - \mathop C\limits^ \oplus H - C{H_3}}\limits_I $
$\mathop {C{H_3} - \mathop C\limits^ \oplus H - OC{H_3}}\limits_{II} $
$\mathop {C{H_3} - \mathop C\limits^ \oplus H - C{H_2} - OC{H_3}}\limits_{III} $
- 10View Solutionનીચેના ઘટકોનો સ્થાયિતાનો સાચો ક્રમ જણાવો;
