બંદુક દ્વારા ગોળી પર લાગતું બળ $F =\left(100-0.5 \times 10^{5} t \right) N$ છે.ગોળી $400 \,m / s$ નાં વેગથી બહાર આવે છે.જ્યારે ગોળી પર બળ શૂન્ય થાય. ત્યારે બળનો આઘાત ($N - s$ માં) કેટલો હશે?
AIIMS 2019, Medium
c
Consider the given expression.
Consider the given expression.
\(F =\left(100-0.5 \times 10^{5} t \right) N\)
Given that, \(F =0\)
\(\left(100-0.5 \times 10^{5} t \right)=0\)
\(t =\frac{100}{0.5 \times 10^{5}}\)
\(=2 \times 10^{-3} sec\)
Calculate the impulse as,
\(I =\int Fdt\)
\(=\int\left(100-0.5 \times 10^{5} t \right) dt\)
\(=\left[100 t -\frac{10^{5}}{2} \frac{ t ^{2}}{2}\right]\)
\(=\left[100\left(2 \times 10^{-3}\right)-\frac{10^{5}}{2} \frac{\left(2 \times 10^{-3}\right)^{2}}{2}\right]\)
\(=0.1 Ns\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
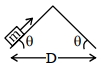
- 1નીચે દર્શાવેલ ઘર્ષણરહિત સપાટી પર એક $m$ દળનો બ્લોક $2\, {N}$ બળની અસર હેઠળ અચળ વેગથી ગતિ કરે છે, તો લગાવેલ બળ વિરુદ્ધ અંતરનો ગ્રાફ કેવો મળે?View Solution
- 2માલગાડીમાં ખુલ્લો ડબ્બો $10 \,m / s$. નાં નિયમિત વેગ સાથે ગતિ કરી રહ્યું છે. જો વરસાદ $5 \,kg / s$ ની દરે શૂન્ય વેગ સાથે પાણી ઉમેરતો હોય, તો પછી ગાડીના સમાન વેગને જાળવવા માટે એન્જિન દ્વારા પુરું પાડવામાં આવતું જરુરી વધારાનું બળ ............ $N$ છે.View Solution
- 3લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec$ ના વેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.View Solution
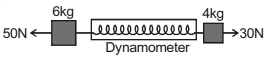
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ડાયનામોમીટર $D$ ને $6 \,kg$ અને $4 \,kg$ ઘળનાં બે બ્લોક્સ સાથે જોડેલ છે. ડાયનામોમીટરનું વાંચન .......... $N$ છે.View Solution
- 5$60 \,kg$ નો એક વ્યક્તિ રસ્તા ઉપર દોડે છે અને એકદમ જ $120 \,kg$ દળ ધરાવતી સ્થિર ટ્રોલી કારમાં કૂદકો મારે છે. પછી, ટ્રોલી કાર $2 \,ms ^{-1}$ ના વેગથી ગતિ કરવાનું શરૂ કરે છે. જ્યારે માણસ કારની અંદર કૂદકો મારે છે ત્યારે દોડતા માણસનો વેગ ............ $ms ^{-1}$ હશે.View Solution
- 6$5\,kg$ દળના એક કણ પર ત્રણ બળો $F_1=10\,N , F_2=8 N$ અને $F_3=6\,N$ લગાડેલા છે. બળ $F_2$ અને $F_3$ લંબરૂપે એવી રીતે લગાડેલા છે કે જેથી કણ સ્થિર રહે. જો બળ $F_1$ ને દૂર કરવામાં આવે, તો કણનો પ્રવેગ ....... $ms^{-2}$ થાય.View Solution
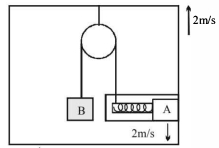
- 7જ્યારે $2\,m / s$ ના વેગથી કરતી મોટરના શાફટ પર દોરી વીંટળાય ત્યારે લિફટનો વેગ $2\,m / s$ છે અને બ્લોક $A$ એ નીચેની દિશામાં $2\,m / s$ ના વેગથી ગતિ કરે છે. તો બ્લોક $B$ નો વેગ $..........$View Solution
- 8$m$ દળ ધરાવતો એક કણ $v_1$ જેટલા અચળ વેગથી ગતિ કરે છે. કણને આઘાત આપતા તેનો વેગ $v_2$ થાય છે. આઘાતનું મુલ્ય કોને બરાબર હશે?View Solution
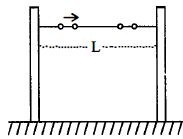
- 9$m$ દળ અને $r$ ત્રિજ્યા ના સમાન મણકાને મોટી સંખ્યા $(n)$ માં એક પાતળા લીસ્સા સમક્ષિતિજ $L\, (L >> r)$ લંબાઈ ના સળિયા માં પરોવેલા છે અને તેઓ યાદચ્છિક રીતે સ્થિર સ્થિતિમાં છે.સળિયાને બે જડ આધાર પર મૂકેલો છે (આકૃતિ જુઓ). તેમાથી એક મણકા ને $v$ જેટલી ઝડપ આપવામાં આવે છે, તો લાંબા સમય પછી દરેક આધાર દ્વારા અનુભવાતું સરેરાશ બળ કેટલું થશે? (ધારો કે દરેક અથડામણ સ્થિતિ સ્થાપક છે.)View Solution
- 10આકૃતિમાં દર્શાવ્યા મુજબ, અનુક્રમે બે દળો $10 \,kg$ અને $20 \,kg$ નો દળરહિત સ્પ્રિંગ સાથે જોડેલ છે , $20\, kg$ દળ પર $200 \;N$ દળ લાગે છે. તે જ સમયે. $10 \,kg$ નો દળ જમણી બાજુ $12 \,m / s ^2$ નો પ્રવેગ ધરાવે છે. તે જ ક્ષણે $20 \,kg$ દળનો પ્રવેગ ................. $m / s ^2$ છેView Solution

