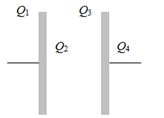
$C$ કેપેસીટન્સ ધરાવતી આઇસોલેટેડ પ્લેટની ચાર સપાટી પરના વિદ્યુત ભારો $Q_1$, $Q_2$, $Q_3$, $Q_4$ આકૃતીમાં દર્શાવ્યા મુજબના છે. તો પ્લેટો વચ્ચેનો વિદ્યુત સ્થિતિમાનનો તફાવત....

Medium
c
વાહક પદાર્થની સમાંતર રહેલી સપાટીઓ સમાન અને વિરૂધ્ધ વિદ્યુતભાર ધરાવે છે.
અહી પ્લેટોનું ક્ષેત્રફળ સમાન છે. \(Q_2 = -Q_3\)
કેપેસીટર પરનો વિદ્યુતભાર એટલે પ્લેટની અંદરની સપાટી પરનો વિદ્યુતભાર (અહી \(Q_2\) થી)
વાહક પદાર્થની સમાંતર રહેલી સપાટીઓ સમાન અને વિરૂધ્ધ વિદ્યુતભાર ધરાવે છે.
અહી પ્લેટોનું ક્ષેત્રફળ સમાન છે. \(Q_2 = -Q_3\)
કેપેસીટર પરનો વિદ્યુતભાર એટલે પ્લેટની અંદરની સપાટી પરનો વિદ્યુતભાર (અહી \(Q_2\) થી)
પ્લેટો વચ્ચેનું વિદ્યુતસ્થિતિમાન=વિદ્યુતભાર/કેપેસીટન્સ \( = \frac{{{Q_2}}}{C} = \frac{{2{Q_2}}}{{2C}}\, = \frac{{{Q_2} - ( - {Q_2})}}{{2C}} = \frac{{{Q_2} - {Q_3}}}{{2C}}.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$16\ \mu F, 1000\ V$ કેપેસિટર લગાવવાનો છે.પરંતુ આપણી પાસે $8\ \mu F$, $250\ V$ ના કેપેસિટર હોય તો, આવા કેટલા કેપેસિટરની જરુર પડે?View Solution
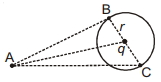
- 2$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 3બે સમ અક્ષયી ટૂંકી વિદ્યુત ડાયપોલ જેમના કેન્દ્રો એકબબીજાથી $R$ અંતરે છે, તેમની વચ્ચે લાગતું બળ કોની સાથે બદલાય છે?View Solution
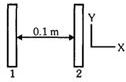
- 4બે અલગ કરેલી (અવાહકીય) પ્લેટોને સમાન રીતે એવી રીતે વિદ્યુતભારીત કરેલ છે. કે જેથી તેમની વચ્ચેનો સ્થિતિમાન તફાવત $V_2$ - $V_1$ = $20\ V$. પ્લેટ $2$ ઉંચા સ્થિતિમાન છે. પ્લેટોને $= 0.1\ m$ અંતરે અલગ કરેલી અનંત રીત વિશાળ (વિસ્તૃત) ગણી શકાય છે. પ્લેટ $1$ ની અંદરની પસાર પર સ્થિત સ્થિતિએ રહેલા એક ઈલેકટ્રોનને મુક્ત કરવામાં આવે છે. જે જ્યારે પ્લેટને અથડાય ત્યારે તેની ઝડપ કેટલી છે.View Solution
$ (e = 1.6 × 10^{-19}\ C, m_0= 9.11 × 10^{-31}\ kg)$
- 5બે સમાન વાહક ગોળાઓ $A$ અને $B$ એકબીજાથી $5 \;cm$ અંતરે મૂકેલા છે તથા સમાન રીતે વિદ્યુતભારીત કરેલાં છે. તેમની ત્રિજ્યાઓ અનુક્રમે $1\; mm$ અને $2 \;mm$ છે. જો બંને ગોળાને વાહકતાર વડે જોડવામાં આવે, તો સંતુલિત સ્થિતિમાં ગોળા $A$ અને $B$ ની સપાટી પરનાં વિદ્યુતક્ષેત્રોનો ગુણોત્તર કેટલો થાય?View Solution
- 6દરેક $40 \,\mu F$ ના બે સંઘારકોને શ્રેણીમાં જોડવામાં આવેલા છે. બે માંથી કોઈ એક સંઘારકને $K$ જેટલા ડાયઈલેક્ટ્રિક અચળાંક ઘરાવતા અવાહક વડે એવી રીતે ભરવામાં આવે છે કે જેથી તંત્રની સમતુલ્ય સંઘારકતા $24 \,\mu F$ થાય. $K$ નું મૂલ્ય ......... હશે.View Solution
- 7આ પ્રશ્નમાં વિધાન $1$ અને વિધાન $2$ છે. વિધાનો પછી આપેલા ચાર વિકલ્પોમાંથી બન્ને વિધાનોને શ્રેષ્ઠ રીતે વર્ણવતું એક વિકલ્પ પસંદ કરો. $R$ ત્રિજ્યા ધરાવતો અવાહક નકકર ગોળો સમાન ધન વીજભાર ઘનતા $\rho $ ધરાવે છે. આ સમાન વિદ્યુતભાર વિતરણને લીધે ગોળાના કેન્દ્ર પાસે, ગોળાની સપાટી પર, અને ગોળાની બહારના બિંદુ પાસે પણ સિમિતિ મૂલ્યનું વિદ્યુત સ્થિતિમાન છે. અનંત અંતરે વિદ્યુત સ્થિતિમાન શૂન્ય છે.View Solution
વિધાન$-1$ : જ્યારે $‘q’$ વિદ્યુતભારને ગોળાના કેન્દ્રથી ગોળાની સપાટી પર લઇ જવામાં આવે ત્યારે તેની સ્થિતિઊર્જા $\frac{{q\rho }}{{3{\varepsilon_0}}}$ વડે બદલાય છે.
વિધાન $-2$ : ગોળાના કેન્દ્રથી $r (r < R)$ અંતરે વિદ્યુતક્ષેત્ર $\frac{{\rho r}}{{3{\varepsilon _0}}}$ છે.
- 8બે કેપેસિટરો $C_1$ અને $C_2$ ને અનુક્રમે $120\ V$ અને $200\ V$ ચાર્જ કરેલ છે. તે જાણવામાં આવ્યું છે કે બંનેને એકબીજાને જોડતાં દરેક એક પરનો સ્થિતિમાન શૂન્ય બનાવી શકાય તેથી.....View Solution
- 9અવકાશમાં $\vec E\, = (25 \hat i + 30 \hat j)\,NC^{-1}$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. જો ઉગમબિંદુ આગળ વિદ્યુતક્ષેત્ર શૂન્ય હોય તો $x\, = 2\, m, y\, = 2\, m$ બિંદુ આગળ વિદ્યુતસ્થિતિમાન $volt$ માં કેટલું મળે?View Solution
- 10એક સમબાજુ ત્રિકોણનાં શિરોબિંદુઓ પર અનુક્રમે $q,q$ અને $-2 q$ જેટલો વિદ્યુતભાર રાખેલ છે. સમબાજુ ત્રિકોણની બાજુની લંબાઈ $L$ છે. કોઈપણ પ્રકારની પ્રવેગરહિત ગતિ દ્વારા આા ત્રણેય વિદ્યુતભારને એકબીજાથી દૂર કરવા માટે બાહ્ય ચાર્જ દ્વારા કરવામાં આવતું કાર્ય કેટલું થશે?View Solution
