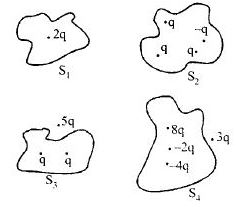
The net fluw linked with closed surfaces \(S_{1}\), \(\mathrm{S}_{2}, \mathrm{S}_{3} \& \mathrm{S}_{4}\) are
For surface \(S_{1}, \phi_{1}=\frac{1}{\varepsilon_{0}}(2 q)\)
For surface
\(\mathrm{S}_{2}, \phi_{2}=\frac{1}{\varepsilon_{0}}(\mathrm{q}+\mathrm{q}+\mathrm{q}-\mathrm{q})=\frac{1}{\varepsilon_{0}} 2 \mathrm{q}\)
For surface \(S_{3}, \phi_{3}=\frac{1}{\varepsilon_{0}}(q+q)=\frac{1}{\varepsilon_{0}}(2 q)\)
For surface
\(S_{4}, \phi_{4}=\frac{1}{\varepsilon_{0}}(8 q-2 q-4 q)=\frac{1}{\varepsilon_{0}}(2 q)\)
Hence, \(\phi_{1}=\phi_{2}=\phi_{3}=\phi_{4}\) i.e. netelectric flux is same for all surfaces.
Keep in mind, the electric field due to a charge outside \(\left(\mathrm{S}_{3} \text { and } \mathrm{S}_{4}\right),\) the Gaussian surface contributes zero net flux through the surface, because as many lines due to that charge enter the surface as leave it.
Download our appand get started for free
Similar Questions
- 1બે વિદ્યુતભારો $4q$ અને $q,\;l$ અંતરે આવેલા છે. એકબીજો $Q$ વિદ્યુતભાર ને તેમની વચ્ચે (મધ્યબિંદુ આગળ) મૂકેલ છે. જો $q$ પરનું પરિણામી બળ શૂન્ય હોય તો $Q$ નું મૂલ્ય ...... છે.View Solution
- 2$p$ ડાયપોલ મોમેન્ટ ધરાવતા ડાયપોલનું કેન્દ્ર ઉદ્ગમબિંદુ પર રહે તે રીતે $x$-અક્ષ પર મૂકેલ છે.ડાયપોલના કેન્દ્રથી અમુક અંતરે આવેલા બિંદુને જોડતી રેખાએ $x$-અક્ષ સાથે બનાવેલો ખૂણો $\theta $ છે.તો તે બિંદુએ વિદ્યુતક્ષેત્રએ $x$-અક્ષ સાથે કેટલો ખૂણો બનાવે? [ $\tan \alpha = \frac{1}{2}\tan \theta $ ]View Solution
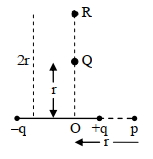
- 3વિધુત દ્રી-ધ્રુવી ને કારણે $P$ બિંદુ આગળ વિધુતક્ષેત્ર $E$ મળે છે સમરેખસ્થ એવા $R$ બિંદુએ વિધુતક્ષેત્ર $\frac{E}{x}$.નું મૂલ્ય. . . . . . હશે:View Solution
- 4$q$ અને $3q$ વિદ્યુતભાર ધરાવતા બે કણો હવામાં $'r' $અંતરે ગોઠવેલા છે. $q$ વિદ્યુતભારથી ' $x$ ' અંતરે વિદ્યુત ક્ષેત્ર શૂન્ય છે. તો $x $નું મૂલ્ય........View Solution
- 5View Solutionદ્વિ ધ્રુવીય ચાકમાત્રાનો એકમ ......... છે.
- 6$+7\ \mu C$ અને $-5\ \mu C$ વિદ્યુતભાર ધરાવતા બે બોલ એકબીજાને $F$ બળ સાથે આકર્ષે છે. જો બંનેમાં $-2\ \mu C$ વિદ્યુતભાર ઉમેરવામાં આવે તો તેમની વચ્ચેનું બળ કેટલું હશે ?View Solution
- 7સમાન $m$ દળ અને સમાન વિદ્યુતભાર $q$ ને $16\, cm$ અંતરે રહેલા છે.તે બંને પર લાગતું બળ શૂન્ય હોય,તો $\frac{q}{m} =$ ______View Solution
- 8અવગણ્ય કદ ધરાવતાં બે એક સરખા વીજભારિત ગોળાઓ અનુક્રમે $2.1\, nC$ અને $-0.1\, nC$ વીજભાર ધરાવે છે. બંનેને એકબીજાનાં સંપર્કમાં લાવી $0.5$ મીટર અંતર માટે જુદા પાડવામાં આવે છે. બંને ગોળાઓ વચ્ચે ઉદ્દભવતું સ્થિત વિદ્યુત બળ $.......... \, \times 10^{-9} \,N$ છે. [ $4 \pi \varepsilon_{0}=\frac{1}{9 \times 10^{9}} SI$ એકમ આપેલ છે. ]View Solution
- 9ડ્યુટ્રોન અને $\alpha$ - કણ હવામાં એકબીજાથી $1\,\mathop A\limits^o $ અંતરે આવેલા છે. ડ્યુટ્રોનને લીધે $\alpha$ - કણ પર લાગતા વિદ્યુતક્ષેત્રનું મૂલ્ય ........ હશે.View Solution
- 10$l$ લંબાઇની રેખા પર $q$, $Q$ અને $4q$ વિદ્યુતભારને એક છેડાથી અનુક્રમે $0,\,\frac {l}{2}$ અને $l$ અંતરે મૂકેલા છે. જો વિજભાર $q$ પર લાગતું બળ શૂન્ય કરવું હોય તો $Q$ વિજભાર કેટલો હોવો જોઈએ?View Solution
