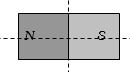
ચુંબકનો આવર્તકાળ $ T$ છે.હવે ચુંબકને આકૃત્તિ મુજબ કાપીને એક ટુકડો દોલનો કરાવતાં તેનો આવર્તકાળ કેટલો થાય?

Diffcult
c
(c)When magnet of length \(l \) is cut into four equal parts. then \(m' = \frac{m}{2}\) and \(l' = \frac{l}{2};\;\;\therefore \;M' = \frac{m}{2} \times \frac{l}{2} = \frac{{ml}}{4} = \frac{M}{4}\)
New moment of inertia \(I' = \frac{{{\rm{w}}{l^2}}}{{12}} = \frac{{\frac{{\rm{w}}}{4}.{{\left( {\frac{1}{2}} \right)}^2}}}{{12}} = \frac{1}{{16}}.\frac{{{\rm{w}}{l^2}}}{{12}}\)
Here \(w\) is the mass of magnet.
\(\therefore \,I' = \frac{1}{{16}}I\); Time period of each part \(T' = 2\pi \sqrt {\frac{{I'}}{{M'{B_H}}}} \)
\( = 2\pi \sqrt {\frac{{I/16}}{{(M/4){B_H}}}} = 2\pi \sqrt {\frac{I}{{4M{B_H}}}} = \frac{T}{2}\)
(c)When magnet of length \(l \) is cut into four equal parts. then \(m' = \frac{m}{2}\) and \(l' = \frac{l}{2};\;\;\therefore \;M' = \frac{m}{2} \times \frac{l}{2} = \frac{{ml}}{4} = \frac{M}{4}\)
New moment of inertia \(I' = \frac{{{\rm{w}}{l^2}}}{{12}} = \frac{{\frac{{\rm{w}}}{4}.{{\left( {\frac{1}{2}} \right)}^2}}}{{12}} = \frac{1}{{16}}.\frac{{{\rm{w}}{l^2}}}{{12}}\)
Here \(w\) is the mass of magnet.
\(\therefore \,I' = \frac{1}{{16}}I\); Time period of each part \(T' = 2\pi \sqrt {\frac{{I'}}{{M'{B_H}}}} \)
\( = 2\pi \sqrt {\frac{{I/16}}{{(M/4){B_H}}}} = 2\pi \sqrt {\frac{I}{{4M{B_H}}}} = \frac{T}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટક એ શિરોલંબ ધટક જેટલો છે.તો તે સ્થળે ડીપ એન્ગલ કેટલા .....$^o$ હશે?View Solution
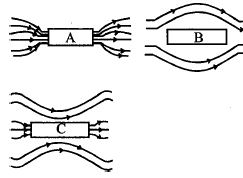
- 2ત્રણ એકસરખા ગજિયા ચુંબક $A, B$ અને $C$ અલગ અલગ પ્રકારના ચુંબકીય દ્રવ્યમાંથી બનેલા છે. જ્યારે તેમણે એકસમાન ચુંબકીયક્ષેત્રમાં મૂકવામાં આવે ત્યારે તેમાં ચુંબકીયક્ષેત્ર રેખા નીચે મુજબ વર્તે છે. આ ત્રણ ગજિયા ચુંબકને તેના ચુંબકીય દ્રવ્ય ડાઈમેગ્નેટિક $(D)$, ફેરોમેગ્નેટિક $(F)$ અને પેરામેગ્નેટિક $(P)$ મુજબ ગોઠવો.View Solution
- 3એક સ્થળે ચુંબક $ 1$ મિનિટમાં $30 $ દોલનો કરે છે.તો જયાં ચુંકીયક્ષેત્ર બમણું હોય,ત્યાં તેનો આવર્તકાળ કેટલો થાય?View Solution
- 4નીચે બે વિધાનો આપેલા છે; એક ને કથન $A$ તરીકે અને બીજાને કારણ $R$ તરીકે સૂચિત લેબલ કરવામાં આવેલ છે.View Solution
કથન $A :$ વીજ ચુંબકો નરમ લોખંડના બનેલા છે.
કારણ $R:$ નરમ લોખંડ ઉચ્ય પારગમ્યતા અને નીચી રિટેન્ટીવીટી ધરાવે છે.
ઉપર્યુક્ત કથનો સંદર્ભમાં, નીયે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 5પાતળા ચુંબકને મુક્ત રીતે લટકાવતા તેના દોલનોનો આવર્તકાળ $T$ મળે છે. હવે તેને બે સમાન ભાગમાં વિભાજિત કરવામાં આવે છે.(બન્નેની લંબાઈ મૂળ લંબાઈ કરતાં અડધી છે) અને તેમાંથી એક ભાગને સમાન ક્ષેત્રમાં મુક્ત રીતે લટકાવતા તે $T'$ આવર્તકાળથી દોલનો કરે છે તો $\frac{{T'}}{T}$ નો ગુણોત્તર કેટલો થાય?View Solution
- 6$m $ ધુવમાન ધરાવતા ગજિયા ચુંબકને લંબાઇ અને પહોળાઇ અડધી થાય,તે રીતે ચાર ભાગમાં વિભાજીત કરતાં એક ટુકડાનું ધ્રુવમાન કેટલું થાય?View Solution
- 7ગજિયા ચુંબકની અક્ષ પર $x $ અંતરે અને વિષુવવૃત્ત રેખા પર $y$ અંતરે ચુંબકીયક્ષેત્ર સમાન હોય,તો $ x $ અને $ y$ નો ગુણોત્તર કેટલો થાય?View Solution
- 8બે સ્થળોએ ડીપ એન્ગલ $30^o$ અને $45^o$ છે.તો પૃથ્વીના ચુંબકીયક્ષેત્રનો સમક્ષિતિજ ઘટકનો ગુણોત્તર કેટલો થાય?View Solution
- 9એક ચુંબકનો આવર્તકાળ $ 2 \,sec$ છે.પૃથ્વીના ચુંબકીય ક્ષેત્રનો સમક્ષિતિજ ઘટક $H$ છે. હવે તેના પર બાહય ચુંબકીય ક્ષેત્ર $F$ લગાવતા નવો આવર્તકાળ $1\, sec$ થાય છે.તો $H/F$ કેટલું થાય?View Solution
- 10$5 \,cm$ લંબાઇ અને $1 \,cm$ વ્યાસ ધરાવતા સળિયાનું મેગ્નેટાઇઝેશન $5.30 × 10^3\,Amp/m^3.$ હોય,તો મેગ્નેટીક મોમેન્ટ કેટલી થાય?View Solution
