$d _1$ અને $d _2$ ઘનતા ધરાવતા પ્રવાહી એ સમાન દબાણ તફાવત હેઠળ આદર્શ કેપિલરી ટ્યુબમાં વહે છે.પ્રવાહીનું સમાન પ્રમાણ (દળ) વહન કરવા માટે લાગેલો સમય $t _1$ અને $t _2$ હોય, પ્રવાહીના શ્યાનતા ગુણાંકનો ગુણોતર $......... $
Medium
a
(a)
(a)
According to poiseuille's equation, Volume of liquid flowing per second in a capillary tube is given by
\(Q =\frac{ V }{ t }=\frac{\pi r ^4 \Delta P }{8 \eta L }\)
So mass of liquid flowing in a capillary tube is given by
\(Q _{ m }=\frac{ m }{ t }=\frac{\pi r ^4 \Delta P }{8 \eta L } d\)
\(\Rightarrow \frac{ m _1}{ t _1}=\frac{\pi r ^4 \Delta P }{8 \eta_1 L } d _1 \ldots(I)\)
\(\Rightarrow \frac{ m _2}{ t _2}=\frac{\pi r ^4 \Delta P }{8 \eta_2 L } d _2 \ldots(II)\)
Dividing \((I)\) by \((II)\), we have
\(\frac{ t _2}{ t _1}=\frac{ d _1}{ d _2} \times \frac{\eta_2}{\eta_1}\)
\(\Rightarrow \frac{\eta_1}{\eta_2}=\frac{ d _1 t _1}{ d _2 t _2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કોઇ લાંબા નળાકારીય પાત્રમાં પ્રવાહી અડધે સુધી ભરેલ છે. જ્યારે પાત્ર પોતાની ઉર્ધ્વ અક્ષને અનુલક્ષીને પરિભ્રમણ કરે છે ત્યારે દિવાલની નજીક (અડીને) પ્રવાહી ઊપર ચઢે છે. જો પાત્રની ત્રિજ્યા $5 \,cm$ અને તેની ચાક ઝડપ $ 2$ ભ્રમણ પ્રતિ સેકન્ડ હોય તો તેના કેન્દ્ર (મધ્યભાગ) અને છેડાની વચ્ચે ઊંચાઈનો તફાવત, $cm$ માં કેટલો હશે?View Solution
- 2એક ઘરની છત પર રહેલી $750\,cm^{2}$ ક્ષેત્રફળ ધરાવતી પાણીની ટાંકીમાં પાણીનું લેવલ પાઈપ ઉપર નળના સ્તરથી ઊંચે રહેલ છે. $500\,nm^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો નળ જ્યારે ખુલ્લો હોય ત્યારે નળમાંથી બાહર નીકળતા પાણીનો વેગ $30\,cm/s$ છે. આ સમયે $\frac{dh}{dt}$ નું મૂલ્ય $x \times 10^{-3}\,m/s$ છે. $x$ નું મૂલ્ય $...........$ હશે.View Solution
- 3સ્નિગ્ધ પ્રવાહીમાં $a$ ત્રિજ્યાના ગોળાનો ટર્મિનલ વેગ કોના સમપ્રમાણમાં હોય?View Solution
- 4સ્પ્રે પમ્પના નળાકારની ટયૂબની ત્રિજયા $R$ છે, તેના એક છેડે $r$ ત્રિજયાના $n$ સૂક્ષ્મ છિદ્રો છે. જો ટયૂબમાં પ્રવાહીની ઝડપ $v$ હોય, તો આ છિદ્રોમાંથી બહાર નીકળતા પ્રવાહીની ઝડપ કેટલી હશે?View Solution
- 5ત્રાજવામાં મૂકેલા બે પદાર્થો પાણીમાં સમતોલનમાં રહે છે,એક પદાર્થનું દળ $36 g $ અને ઘનતા $9 g / cm^3$ છે,જો બીજા પદાર્થનું દળ $ 48 g$ હોય,તો ઘનતા .......$g / cm^3$ થાય.View Solution
- 6અરોપ્લેનની સમક્ષિતિજ સમતલમાં રહેલી પાંખ ઉપરની સપાટી પર હવાની ઝડપ $60 \,m / s$ અને તળિયાની સપાટી નીચે તે $45 \,m / s$ છે. જો હવાની ઘનતા $1.293 \,kg / m ^3$ છે તો દબાણનો તફાવત ............ $N/m^2$ છેView Solution
- 7બરફની ઘનતા $0.9 \,g / cm ^3$ છે. તો પાણીની બહાર તરતા બરફનું ......... $\%$ કદ બહાર હશે ?View Solution
- 8જ્યારે બ્લોક હવામાં હોય ત્યારે સ્પ્રિંગ માપન $60 \,N$ છે. જ્યારે તેને પાણીની અંદર નાખવામાં આવે ત્યારે તેનું માપન $40 \,N$ છે. તો બ્લોકનું વિશિષ્ટ ઘનતા કેટલું ?View Solution
- 9જો પાઈપમાંથી વહન પામતા પાણીની ઝડપ $2 \,m / s$ હોય તો તેની એકમ કદ દીઠ ગતિ ઊર્જા ......... $J/m^3$View Solution
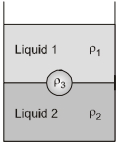
- 10એક બરણીમાં, એકબીજામાં મિશ્રિત ન થઇ શકે તેવાં તથા $\rho_{1}$ અને $\rho_{2}$ ધનતાવાંં બે પ્રવાહી ભરેલાં છે. આ બરણીમાં $\rho_{3}$ ધનતાવાળો ગોળો નાખતા તે આકૃતિમાં દર્શાવ્યા મુજબની સંતુલન સ્થિતિ પ્રાપ્ત કરે છે. તો નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.View Solution