ત્રાજવામાં મૂકેલા બે પદાર્થો પાણીમાં સમતોલનમાં રહે છે,એક પદાર્થનું દળ $36 g $ અને ઘનતા $9 g / cm^3$ છે,જો બીજા પદાર્થનું દળ $ 48 g$ હોય,તો ઘનતા .......$g / cm^3$ થાય.
Diffcult
c
(c)Apparent weight \( = V(\rho - \sigma )g = \frac{m}{\rho }(\rho - \sigma )g\)
where \(m = \) mass of the body,
\(\rho = \) density of the body
\(\sigma = \) density of water
If two bodies are in equilibrium then their apparent weight must be equal.
\(\therefore \) \(\frac{{{m_1}}}{{{\rho _1}}}({\rho _1} - \sigma ) = \frac{{{m_2}}}{{{\rho _2}}}({\rho _2} - \sigma )\)
==> \(\frac{{36}}{9}(9 - 1) = \frac{{48}}{{{\rho _2}}}({\rho _2} - 1)\)
By solving we get \({\rho _2} = 3\).
(c)Apparent weight \( = V(\rho - \sigma )g = \frac{m}{\rho }(\rho - \sigma )g\)
where \(m = \) mass of the body,
\(\rho = \) density of the body
\(\sigma = \) density of water
If two bodies are in equilibrium then their apparent weight must be equal.
\(\therefore \) \(\frac{{{m_1}}}{{{\rho _1}}}({\rho _1} - \sigma ) = \frac{{{m_2}}}{{{\rho _2}}}({\rho _2} - \sigma )\)
==> \(\frac{{36}}{9}(9 - 1) = \frac{{48}}{{{\rho _2}}}({\rho _2} - 1)\)
By solving we get \({\rho _2} = 3\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બરફની ઘનતા $0.9 \,g / cm ^3$ છે. તો પાણીની બહાર તરતા બરફનું ......... $\%$ કદ બહાર હશે ?View Solution
- 2એક પ્રયોગમાં એક નાનો સ્ટીલનો બોલ પ્રવાહીમાં $10\, cm/s$ ની અચળ ઝડપથી પડે છે. જો બૉલને ઉપર તેના અસરકારક વજનથી બમણા બળથી ખેચવામાં આવે તો તે ....... $cm/s$ ઝડપથી ઉપર ગતિ કરશે?View Solution
- 3$0.1 \,m ^2$ ક્ષેત્રફળ ધરાવતી સમતલ પ્લેટને સમતલ સપાટી પર મૂકેલી છે અને તે $10^{-5 }\,m$ જાડાઈની તેલની ફિલ્મ વડે સપાટીથી અલગ કરેલી છે. જેની શ્યાનતા પ્લેટને $1.5 \,N sm ^{-2}$ છે. $1 \,mm s ^{-1}$ અચળ ઝડપથી સપાટી પર ગતિ કરાવવા માટે જરરી બળ ........ $N$ હશે.View Solution
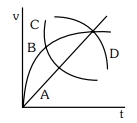
- 4એક ગોળાકાર બોલને ખુબજ સ્નિગ્ધ પ્રવાહીના લાંબા સ્તંભમાં મુક્ત (છોડવામાં)કરવામાં આવે છે.આકૃતિમાં દર્શાવેલ વક્ર,કે જે બોલ માટે ઝડપ $(v)$ અને સમય $(t)$ના વિધેય તરીકે દર્શાવે તે$........$છે.View Solution
- 5જમીન પર રાખેલ ટાંકીમાં $10\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તેમાં બે જમીનથી $3\, m$ અને $7\, m$ ઊંચાઈ કાણાં પડેલા છે.તો બહાર આવતા પાણી માટે શું કહી શકાય?View Solution
- 6તમે એક ઓલિક ઍસિડનું મંદ દ્રાવણ લીધું છે કે જેમાં પ્રતિ $cm ^{3}$ દ્રાવણમાં ઓલિક ઍસિડનું પ્રમાણ $0.01 \,cm ^{3}$ છે. $\left(\frac{3}{40 \pi}\right)^{\frac{1}{3}} \times 10^{-3}\; cm$ ત્રિજ્યાના દ્રાવણના $100$ ટીપાંથી $4\;cm ^{2}$ ક્ષેત્રફળ ધરાવતું પાતળું સ્તર બનાવવામાં આવે છે. તેમાં ઓલિક એસિડની જાડાઈ $x \times 10^{-14} \;m$ છે. જ્યાં $x$ કેટલું હશે?View Solution
- 7View Solutionઆડી પાઈપનો આડછેદનું ક્ષેત્રફળ સમાન નથી, તો પ્રવાહી માટે આ પાઈપમાં નીચેનામાંથી ક્યો સમય બદલાતો નથી?
- 8View Solutionદબાણ માટે ખોટું નિવેદન પસંદ કરો.
- 9પાણીની અંદર $1\,cm$ ત્રિજ્યાના હવાના પરપોટાનો ઉપરની દિશામાંનો પ્રવેગ $9.8\, cm\, s ^{-2}$ છે. પાણીની ઘનતા $1\, gm\, cm ^{-3}$ અને પાણી દ્વારા પરપોટા પર નહિવત ઘર્ષણબળ લાગે છે. તો પરપોટાનું દળ $.......gm$ હશે.View Solution
$\left( g =980 \,cm / s ^{2}\right)$
- 10$0.4\, m ^{2}$ આડછેદ નું ક્ષેત્રફળ ધરાવતી પાણીની ટાંકીમાં તળિયે $1\, cm ^{2}$ આડછેદ વાળો વાલ્વ છે . પાત્ર માં $40\, cm$ ઊંચાઈ સુધી પાણી ભરેલ પિસ્ટન પર $24\, kg$ પદાર્થ મૂકીને વાલ્વ નો ખૂલતાં પાણી ના વેગથી બહાર આવે તો $V$......$m/s$View Solution