દડાનું દળ સળિયાનાં દળ કરતાં $\frac{9}{5}$ ગણું છે,સળિયાની લંબાઈ $1\;m$ છે, દડાનું લેવલ એ સળિયાના નીચેના છેડે છે, દડાને સળિયાના ઉપરના છેડે પહોચવા માટે લાગતો સમય(સેકન્ડ માં) શું હશે?
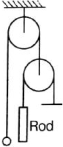

AIIMS 2018, Diffcult
a
Let \(a_{1}\) and \(a_{2}\) be accelerations of a ball (upward) and rod (downward), respectively.
Let \(a_{1}\) and \(a_{2}\) be accelerations of a ball (upward) and rod (downward), respectively.
Clearly, from the diagram
\(2 a_{1}=a_{2} \ldots( i )\)
Now, for the ball
\(2 T-\frac{9}{5} m g-\frac{9}{5} m a-(i i)\)
and for the rod, \(m g-T=m a_{2} \ldots\) \((iii)\)
On solving equations \((i)\) and \((iii),\) we get
\(a_{1}=\frac{g}{29} m / s^{2} \uparrow\) (upward)
\(a_{2}=\frac{2 g}{29} m / s ^{2} \downarrow\) (upward)
So, acceleration of ball \(w.r.t\) rod \(=a_{1}+a_{2}=\frac{3 g}{29}\)
Now, displacement of ball \(w.r.t.\) rod when it reaches the upper end of rod is \(1\, m\).
Using equation of motion,
\(s=u t+\frac{1}{2} a t^{2}\)
\(s=0+\frac{1}{2} \times \frac{3 \times 10}{29} t^{2}\)
\(t=\sqrt{\frac{58}{30}}=1.4 s\) (approx)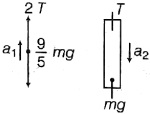
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$50\,kg$ નો વાંદરો, $350\,N$ નું તણાવ $(T)$ સહન કરી શકે તેવા દોરડા ઉપર ચઢે છે. પહેલાં તે $4\,ms ^{-2}$ ના પ્રવેગ થી દોરડા પર નીચે ઉતરે છે અને પછી $5\,ms ^{-2}$ ના પ્રવેગથી દોરડા પર ઉપર ચઢે છે. સાચો વિકલ્પ પસંદ કરો :$\text { ( } g=10\,ms ^{-2})$ લો.View Solution
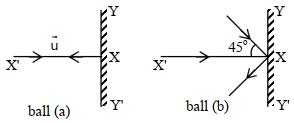
- 2$30 \,{g}$ ના સમાન દળના બે બિલિયર્ડ દડા સમાન $108\, {kmph}$ (આકૃતિમાં દર્શાવ્યા પ્રમાણે) ની ઝડપે દઢ દિવાલ સાથે જુદા જુદા ખૂણે અથડાય છે. જો દડાઓ સમાન ઝડપે પરાવર્તિત થાય, તો $X$ અક્ષની દિશામાં બોલ $a$ અને બોલ $b$ ના આઘાતના મૂલ્યનો ગુણોત્તર કેટલો થાય?View Solution
- 3$0.05\,kg$ નાં બે બિલિયર્ડ બોલ વિરુદ્ધ દિશામાં $10\,ms^{-1}$ સાથે ગતિ કરતાં સંઘાત (અથડામણ) અનુભવે છે અને સમાન ઝડપ સાથે પાછા ફરે છે. જો સંપર્ક સમય $t =0.005\,s$ હોય તો એકબીજાને કારણે પ્રવર્તતું બળ $.......N$ હશે.View Solution
- 4$4 \mathrm{~g}$ અને $25 \mathrm{~g}$ દળના બે પદાર્થ સમાન ગતિ ઉર્જા સાથે ગતિ કરે છે. તેમના રેખીય વેગમાનના મૂલ્યોનો ગુણોત્તર______છેView Solution
- 5એક એલિવેટરની અંદર $2 \,kg$ અને $4 \,kg$ દળના બે બ્લોક્સ આદર્શ ગરગડી પરથી પસાર કરેલી દળરહિત દોરી વડ લટકાવેલાં છે. એલિવેટર એ $\frac{g}{2}$ પ્રવેગ સાથે ઉર્ધ્વ દિશામાં ગતિ કરી રહ્યો છે. બ્લોકો વચ્ચે જોડેલ દોરીમાં ઉદ્ભવવો તણાવ ............ $N$ હશે. $\left(g=10 m / s ^2\right.$ લો).View Solution
- 6લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec$ ના વેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.View Solution
- 7View Solutionજો કોઈ તંત્રનો અંતિમ વેગમાન એ તેના પ્રારંભિક વેગમાનને બરાબર હોય તો
- 8$20 \,kg$ નો વાંદરો ઊભી દોરડું પકડે છે. જો દોરડા પર $25\,kg$ નું દળ લટકાવવામાં આવે, તો દોરડું તૂટતું નથી, પરંતુ જો તેના પર $25\,kg$ થી વધુ દળ લટકાવવામાં આવે તો તે તૂટી જશે. તે મહત્તમ કેટલા પ્રવેગથી ($m/{s^2}$ માં) વાંદરો દોરડા પર ચઢી શકે? $(g = 10\,m/{s^2})$View Solution
- 9View Solutionકાર વળાંક લે ત્યારે માણસ બહાર ફેંકાય,કારણ કે માણસ પર બહાર તરફ બળ લાગે છે.
- 10$10\,kg$ દળવાળી એક મશીન ગનમાંથી $20\,g$ દળની $100\,ms ^{-1}$ ઝડપથી અને $180$ પ્રતિ મિનિટ ના દરથી બુલેટ છોડવામાં આવે છે. તો મશીનગનનો રીકોઈલ વેગ $...........\,m/s$ થાય.View Solution
