ધન $x$-અક્ષ પર, $I$ પ્રવાહનું વહન કરતા તારની લંબાર $L$ છે.તેને $\vec{B}=(2 \hat{i}+3 \hat{j}-4 \hat{k}) T$ ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવે છે. તાર પર લાગતા ચુંબકીય બળનું મૂલ્ય $..........IL$ છે.
NEET 2023, Medium
d
\(\overrightarrow{ F } = I (\vec{\ell} \times \overrightarrow{ B })\)
\(\overrightarrow{ F } = I (\vec{\ell} \times \overrightarrow{ B })\)
\(= I [( L \hat{ i }) \times(2 \hat{ i }+3 \hat{ j }-4 \hat{ k })]\)
\(= I (4 L \hat{ j }+3 L \hat{ k })\)
\(|\overrightarrow{ F }| =5\,IL\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
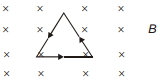
- 1એક તારને $100\,cm$ બાજુના સમભૂજ ત્રિકોણના સ્વરૂપમાં વાળવામાં આવ્યો છે અને $2\;A$ નો વિદ્યુતપ્રવાહ તેમાંથી વહે છે. તેને કાગળના સમતલની અંદર લંબ દિશામાં $2.0\,T$ પ્રેરણના ચુંબકીયક્ષેત્રમાં મૂકવામાં આવ્યો છે. ત્રિકોણની દરેક બાજુ પર લાગતા બળનું મૂલ્ય અને દિશા કેટલી હશે ?View Solution
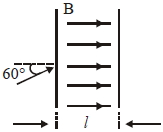
- 2$l$ લંબાઈ માં $0.3\,T$ નું ચુંબકીય ક્ષેત્ર છે. પ્રોટોન આ ક્ષેત્ર સાથે $60$ ના ખૂણે $4 \times 10^{5}\, ms ^{-1}$ ના વેગ થી દાખલ થાય છે. $10$ પરિણામમાં પ્રોટોન $l$ અંતર કાપતો હોય તો $l= ....... m$View Solution
(પ્રોટોનનું દળ $=1.67 \times 10^{-27} \,kg,$ પ્રોટોનનું વિધુતભાર $\left.=1.6 \times 10^{-19}\, C \right)$
- 3પૃથ્વીનું ચુંબકીયક્ષેત્ર $ 0.5 \times {10^{ - 5}}\,Wb{\rm{ - }}{m^{ - 2}} $ છે. $5.0\,cm$ ત્રિજયા ધરાવતી પ્રવાહધારિત રીંગના કેન્દ્ર પર ચુંબકીયક્ષેત્ર શૂન્ય કરવા માટે કેટલા.......$A$ પ્રવાહની જરૂર પડે?View Solution
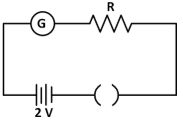
- 4એક ગેલ્વેનોમીટરમાં $50$ કાંપા છે.બેટરીનો આંતરિક અવરોધ શૂન્ય છે. જ્યારે $R = 2400\,\Omega $ જોડેલો હોય ત્યારે ગેલ્વેનોમીટર $40$ કાંપા જેટલું આવર્તન દર્શાવે છે. જ્યારે $R = 4900\,\Omega $ જોડેલો હોય ત્યારે ગેલ્વેનોમીટર $20$ કાંપા જેટલું આવર્તન દર્શાવે છે. તો ઉપરની માહિતી પરથી શું તારણ કાઢી શકાય?View Solution
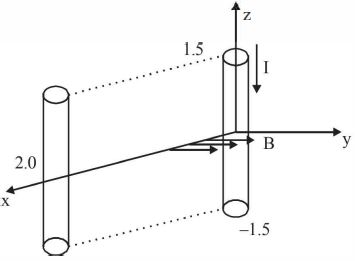
- 5આકૃતિમાં બતાવ્યા પ્રમાણે એક સુવાહક કે જે $Z-$ અક્ષને સમાંતર $-1.5$$ \le Z < 1.5\,m$ વચ્ચે રહેલ છે,જેમાંથી $ - {\hat a_z}$ દિશામાં $10.0$ $A$ નો અચળ પ્રવાહ વહે છે.આપેલ સૂત્ર $\vec B$ $=$ $3.0 \times 10^{-4}$ $e^{-0.2x}$ ${\hat a_y}\,T$ માટે સુવાહકને અચળ ઝડપે $5 \times 10^{-3} $ $ s$ સમય ગાળામાં $x=2.0$ $m$ $,y=0$ $m$ સ્થાને લઇ જવા જરૂરી કાર્ય-દર .......$W$ માં શોધો.આ ગતિ $X-$ અક્ષને સમાંતર છે,એવું ધારો.View Solution
- 6નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ :બાયો-સાર્વટનો નિયમ પ્રવાહ ધરાવતા સુવાહકના ફક્ત અતિસુક્ષ્મ વિદ્યુતખંડ $(Idl)$ ને કારણે ઉત્પન્ન ચુંબકીય ક્ષેત્રની તીવ્રતાનું સૂત્ર આપે છે.
વિધાન $II$ :બાયો-સાર્વટનો નિયમ વીજભાર $q$ માટે કુલંબના પ્રતિવર્ગના નિયમ જેવો જ છે, કે તેમાં પ્રથમ એ અદિશ ઉદગમ $Idl$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે જ્યારે પછીનો એ સદિશ ઉદગમ $q$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય વિક્લ્પ પસંદ કરો.
- 7View Solutionનિયમિત વેગ ધરાવતા એક ઈલક્ટ્રોક પ્રવાહ ધરાવતા લાંબા સોલેનોઈડની અંદર તેની અક્ષની દિશામાં પ્રક્ષિપ્ત કરવામાં આવે છે. તો . . . . . . .
- 8$Z-$ દિશામાં અચળ ચુંબકીયક્ષેત્ર $B=0.3\, T$ પ્રવર્તે છે. $10\, cm\times5\, cm$ પરિમાણ ધરાવતા લંબચોરસ $abcd $ માંથી $I=12\, A$ પ્રવાહ વહે છે. નીચે આપેલા આલેખ પૈકી કયા આલેખમાં તે સ્થાયી સંતુલન સ્થિતિમાં હશે?View Solution
- 9$4.5 \times 10^{5} \;m / s$ના વેગથી ગતિ કરતાં બિંદુવત વિજભારના કારણે ઉત્પન્ન થતાં વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્રનો ગુણોતર કેટલો થાય?View Solution
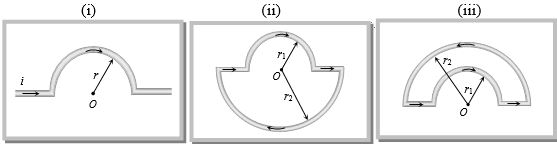
- 10આપેલ પરિપથ માટે $O $ બિંદુ પાસે ચુંબકીયક્ષેત્ર આપેલ છે તો નીચે પૈકી કયું સાચું થાય?View Solution
$(i)$ $(ii)$ $(iii)$ (A) $\frac{{{\mu _0}i}}{r}$ $\otimes$ (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{{2r}}$ $\odot$ (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ (C) $\frac{{{\mu _0}i}}{{4r}}$ $\otimes$ (C) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ (C)$\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ (D) $\frac{{{\mu _0}i}}{{4r}}$ $\odot$ (D) $0$ (D) $0$