દળ $m$ અને $x$ લંબાઈવાળા ગોળા સાથેના એક સાદા લોલકને શિરોલંબ સાથે $\theta_1$ ખૂણો અને ત્યારબાદ $\theta_2$ ખૂણો રાખેલ છે. જ્યારે આ સ્થિતિઓમાંથી છોડવામાં આવે ત્યારે તે નિમ્નત્તમ બિંદૂએ ઝડપો અનુક્રમે $v_1$ અને $v_2$ પસાર કરે છે. તો $\frac{v_1}{v_2}=$ ...... હશે?
Medium
Download our app for free and get started
b
(b)
(b)
\(U_i+k_i=U_f+k_f\)
(Mechanical energy conservation)
\(m g l(1-\cos \theta)=\frac{1}{2} m v^2\)
\(\frac{v_1^2}{v_2^2}=\frac{1-\cos \theta_1}{1-\cos \theta_2}\)
\(\frac{v_1}{v_2}=\sqrt{\frac{1-\cos \theta_1}{1-\cos \theta_2}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$12 kg$ નો સ્થિર બોમ્બ ફૂટતાં $1:3$ દળના $2$ ટુકડા થાય છે.નાના ટુકડાની ગતિઊર્જા $216 J$ હોય,તો મોટા ટુકડાનું વેગમાન કેટલા ............ $ kg-m/sec$ થશે?View Solution
- 2સંપૂર્ણ સ્થિતિસ્થાપક સંધાત માટે રેસ્ટીંટયુશન ગુણાંક $e$ કેટલો હોય છે?View Solution
- 3$m $ દળ અને $ v$ વેગની એક ગોળી $M$ દળના લોલક આગળથી પસાર થાય છે અને $v/2$ વેગ સાથે અથડાય છે. $v$ ની કઈ ન્યૂનત્તમ કિંમત માટે લોલક સંપૂર્ણ ચક્ર પૂર્ણ કરશે ?View Solution
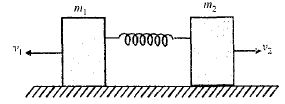
- 4કોઈ સ્પ્રિંગ ને સમક્ષિતિજ ઘર્ષણ રહિત સપાટી પર આકૃતિમાં બતાવ્યા પ્રમાણે બે $m_1$ અને $m_2$ દળ ધરાવતા બે બ્લોક ની વચ્ચે સંકોચન કરવવામાં આવે છે. જ્યારે બ્લોક ને મુક્ત કરવામાં આવે છે, ત્યારે તેનો પ્રારંભિક વેગ $v_1$ and $v_2$ છે. સ્થિર થયા પહેલા બ્લોક દ્વારા કાપેલ અંતર અનુક્રમે $x_1$ અને $x_2$ હોય તો $\left( {\frac{{{x_1}}}{{{x_2}}}} \right)$ નો ગુણોત્તર શું થાય?View Solution
- 5કારને $ F$ અવરોધકબળ લાગતાં $s$ અંતર કાપીને સ્થિર થાય છે.જો કારનું દળ $ 50 \%$ વધે તેા કેટલા.....$s$ અંતરે કાર સ્થિર થશે?View Solution
- 6$m$ દળનો પદાર્થ $v$ વેગથી તે જ દિશામાં $ kv$ વેગથી જતાં $nm $ દળના પદાર્થ સાથે અથડાતા,પ્રથમ પદાર્થ સ્થિર થાય,તો બીજા પદાર્થનો વેગView Solution
- 7$5\, kg$ ના બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.2$ છે,તેના પર $25 \,N $ નું બળ દ્વારા $10 \,m$ ખસેડતાં બ્લોક ........ $J$ ગતિઉર્જા પ્રાપ્ત કરશે.View Solution
- 8$2kg $ નો પદાર્થ $3 m/sec$ ના વેગથી વિરુધ્ધ દિશામાં આવતા $ 4 m/s$ ના $1 kg $ ના પદાર્થ સાથે અથડાતા બંને પદાર્થ ચોંટી જાય છે.તો તેમનો સંયુકત વેગ કેટલો થાય?View Solution
- 9સમય $x$ ના વિધેય તરીકે સમક્ષિતિજ લીસી સપાટી પર $1 \;kg $ દળનો પદાર્થનું સ્થાનાંતર $x = \frac{{{t^3}}}{3}$ સૂત્ર વડેે આપવામાં આવે છે. પ્રથમ એક સેકન્ડ માટે બાહ્ય પરિબળ વડે થતું કાર્ય ........... $J$ છે.View Solution
- 10View Solutionરાઇફલમાથી બુલેટ છોડવામાં આવે છે. જો રાઇફલ મુક્ત રીતે પાછળ તરફ ધકેલાતી હોય તો રાઇફલ ની ગતિ ઉર્જા કેટલી હશે?