
Frequency of \(1\) st harmonic of \(AB\)
\(=\frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}_{\mathrm{AB}}}{\mathrm{m}}}\)
Frequency of \(2\) nd harmonic of \(\mathrm{CD}\)
\(=\frac{1}{\ell} \sqrt{\frac{\mathrm{T}_{\mathrm{CD}}}{\mathrm{m}}}\)
Given that the two frequencies are equal.
\(\therefore \frac{1}{2 \ell} \sqrt{\frac{\mathrm{T}_{\mathrm{AB}}}{\mathrm{m}}}=\frac{1}{\ell} \sqrt{\frac{\mathrm{T}_{\mathrm{CD}}}{\mathrm{m}}}\)
\(\Rightarrow \frac{\mathrm{T}_{\mathrm{AB}}}{4}=\mathrm{T}_{\mathrm{CD}} \Rightarrow \mathrm{T}_{\mathrm{AB}}=4 \mathrm{T}_{\mathrm{CD}}\) \(...(i)\)
For rotational equilibrium of massless rod, taking torque about point \(O.\)
\(\mathrm{T}_{\mathrm{AB}} \times \mathrm{x}=\mathrm{T}_{\mathrm{CD}}(\mathrm{L}-\mathrm{x})\) \(...(ii)\)
For translational equilibrium,
\(\mathrm{T}_{\mathrm{AB}}+\mathrm{T}_{\mathrm{CD}}=\mathrm{mg}\) \(..(iii)\)
On solving, \((i)\) \(\&(iii)\) we get, \(\mathrm{T}_{\mathrm{CD}}-\frac{\mathrm{mg}}{5}\)
\(\therefore \mathrm{T}_{\mathrm{AB}}=\frac{4 \mathrm{mg}}{5}\)
Substituting these values in \((ii)\) we get
\(\frac{4 m g}{5} \times x=\frac{m g}{5}(L-x)\)
\(\Rightarrow 4 \mathrm{x}=\mathrm{L}-\mathrm{x} \Rightarrow \mathrm{x}=\frac{\mathrm{L}}{5}\)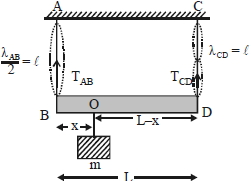
Download our appand get started for free
Similar Questions
- 1નકકર ધાતુના ભોયતયિળા પર $ 1\; m $ લંબાઇનો એક ધાતુનો સળિયો એકદમ શિરોલંબ છોડવામાં આવે છે.ઓસિલોસ્કોપ વડે એ શોધવામાં આવ્યું કે અથડામણ $1.2 \;kHz$ આવૃતિના સંગત તરંગ ઉત્પન્ન કરે છે. આ ધાતુના સળિયામાં ધ્વનિની ઝડપ ($m/s$ માં) કેટલી હશે?View Solution
- 2દોરી $75.0\, cm$ અંતરે રહેલા બે જડિત આધાર વચ્ચે બાંધેલી છે. તેની આવૃતિ $420\, Hz$ અને $315\, Hz$ છે. તેની વચ્ચે બીજી આવૃતિ આવતી નથી તો તેની લઘુત્તમ આવૃતિ ($Hz$ માં) કેટલી હશે?View Solution
- 3પર્વત તરફ ગતિ કરતો કારનો ચાલક $600 \,Hz$ આવૃતિનો હોર્ન વગાડે છે. કારની ઝડપ $30 \,m / s$ છે. અને હવામાં અવાજની ઝડપ $330 \,m / s$ હોય, તો ચાલક દ્વારા સંભળાતા પરાવર્તીત અવાજની આવૃતિ ......... $Hz$ છે.View Solution
- 4એક અનુનાદ નળીમાં બે અનુક્રમિત જગ્યાઓના સ્થાન $15 \,cm$ અને $48 \,cm$ અંતરે છે. જો સ્વરકાંટાની આવૃતિ $500 \,cps$ હોય તો અવાજની ઝડપ ........... $m/s$ હોય.View Solution
- 5હવાના કણોનું સ્થાનાંતર $(s)$ એ ધ્વનિના તરંગ દ્વારા ઉત્પન્ન થતાં દબાણના તફાવત $(\Delta p)$ ના સમપ્રમાણમાં છે. સ્થાનાંતર $(s)$ એ ધ્વનિની ઝડપ $(v),$ હવાની ઘનતા $(\rho)$ અને આવૃતિ $(f)$ પર પણ આધાર રાખે છે. જો $\Delta p \approx 10\, Pa , v \approx 300\, m / s , p \approx 1\, kg / m ^{3}$ અને $f \approx 1000 \,Hz$ હોય તો $s$ નું મૂલ્ય કયા ક્રમનું હશે?View Solution
(ગુણકારનો અચળાંક $1$ લો)
- 6તરંગનું સમીકરણ $y = {10^{ - 4}}\sin \,\left[ {100\,t - \frac{x}{{10}}} \right] $ વડે રજૂ કરવામાં આવે છે. તરંગનો વેગ ($m/s$ માં) કેટલો થાય?View Solution
- 7હુકના નિયમનુ પાલન કરતાં તારની લંબાઈમાં થતો વધારો $x$ છે ખેચાયેલા તાર માં અવાજ ની ગતિ $v$ છે. તાર ની લંબાઈ $1.5x$ કરવામાં આવે તો અવાજ ની ગતિ કેટલી થાય?View Solution
- 8$‘SONAR’$ નીચેનામાંથી કયા તરંગો ઉત્પન્ન કરે છે?View Solution
- 9પ્રગામી તરંગનું સમીકરણ $y = 0.02\,\sin \,2\pi \left[ {\frac{t}{{0.01}} - \frac{x}{{0.30}}} \right]$ મુજબ આપવામાં આવે છે. જ્યાં $x$ અને $y$ મીટરમાં અને $t$ સેકન્ડમાં છે. તો તરંગનો વેગ ($ms^{-1}$ માં) કેટલો હશે?View Solution
- 10$1.5 m$ લંબાઇની બંધ પાઇપની ત્રીજી આવૃત્તિ કેટલી ... $Hz$ થાય? હવામાં ધ્વનિનો વેગ $330 m/s$ છે.View Solution
