Download our app for free and get started
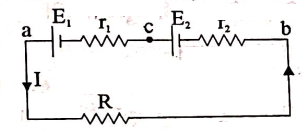
सामने चित्र में $E _1$ व $E _2$ तथा आन्तरिक प्रतिरोध $r _1$ तथा $r _2$ वाले दो सेलों का श्रेणी संयोजन दिखाया गया है। इसके अन्त सिरों को एक बाह्य प्रतिरोध $R$ से जोड़ा गया है। यदि सेलों के संयोजन से प्रतिरोध $R$ में प्रवाहित धारा का मान $I$ है तो ओम के नियम से
$V = IR......(1)$
तथा संयोजन के अन्त बिन्दुओं $a$ व $b$ के मध्य विभवान्तर का मान दोनों सेलों की टर्मिनल वोल्टता के योग के तुल्य होगा, अर्थात्
$V_{a b}=\left(E_1-Ir_1\right)+\left(E_2-Ir_2\right)......(2)$
सिद्धान्त से टर्मिनल वोल्टता; प्रतिरोध R के सिरों पर उत्पन्न विभवान्तर V के बराबर होगी, अतः
$E _1- Ir _1+ E _2- Ir _2= IR$
या $E_1+E_2=I R+I r_1+I r_2$
या $E_1+E_2=I\left(R+r_1+r_2\right)$
या $I=\frac{E_1+E_2}{R+r_1+r_2}=\frac{E_0}{R+r_0}$ ...... (3)
यहाँ $E_0=E_1+E_2$ सेलों के कुल वि.वा. बलों का मान तथा $r_0=$ $\left(r_1+r_2\right)$ सेलों का कुल आन्तरिक प्रतिरोध है, इससे स्पष्ट है -
(i) श्रेणी संयोजन में कुल विद्युत वाहक बल का मान संयोजित सेलों के वि.वा. बलों के योग के तुल्य होता है।
(ii) यदि संयोजन में समान विद्युत वाहक बल व आन्तरिक प्रतिरोध के n सेल जुड़े हुए हों तो बाह्य प्रतिरोध R में प्रवाहित धारा का मान -
$I=\frac{n E}{R+n r}=\frac{E}{r+\frac{R}{n}}$ ......(4)
अर्थात् बाह्य परिपथ में प्रवाहित धारा का मान एक सेल के कारण प्राप्त धारा के मान से अधिक होता है।
(iii) संयोजन में यदि एक बैटरी की ध्रुवता को उलट दिया जाये तो तुल्य वि.वा. बल का मान $\left(E_1-E_2\right)$ या $\left(E_2-E_1\right)$ प्राप्त होता है।
$V = IR......(1)$
तथा संयोजन के अन्त बिन्दुओं $a$ व $b$ के मध्य विभवान्तर का मान दोनों सेलों की टर्मिनल वोल्टता के योग के तुल्य होगा, अर्थात्
$V_{a b}=\left(E_1-Ir_1\right)+\left(E_2-Ir_2\right)......(2)$
सिद्धान्त से टर्मिनल वोल्टता; प्रतिरोध R के सिरों पर उत्पन्न विभवान्तर V के बराबर होगी, अतः
$E _1- Ir _1+ E _2- Ir _2= IR$
या $E_1+E_2=I R+I r_1+I r_2$
या $E_1+E_2=I\left(R+r_1+r_2\right)$
या $I=\frac{E_1+E_2}{R+r_1+r_2}=\frac{E_0}{R+r_0}$ ...... (3)
यहाँ $E_0=E_1+E_2$ सेलों के कुल वि.वा. बलों का मान तथा $r_0=$ $\left(r_1+r_2\right)$ सेलों का कुल आन्तरिक प्रतिरोध है, इससे स्पष्ट है -
(i) श्रेणी संयोजन में कुल विद्युत वाहक बल का मान संयोजित सेलों के वि.वा. बलों के योग के तुल्य होता है।
(ii) यदि संयोजन में समान विद्युत वाहक बल व आन्तरिक प्रतिरोध के n सेल जुड़े हुए हों तो बाह्य प्रतिरोध R में प्रवाहित धारा का मान -
$I=\frac{n E}{R+n r}=\frac{E}{r+\frac{R}{n}}$ ......(4)
अर्थात् बाह्य परिपथ में प्रवाहित धारा का मान एक सेल के कारण प्राप्त धारा के मान से अधिक होता है।
(iii) संयोजन में यदि एक बैटरी की ध्रुवता को उलट दिया जाये तो तुल्य वि.वा. बल का मान $\left(E_1-E_2\right)$ या $\left(E_2-E_1\right)$ प्राप्त होता है।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1सेल के आन्तरिक प्रतिरोध की परिभाषा दीजिए।दो सेल जिनके विद्युत वाहक बल क्रमष: $\varepsilon_1$, $\varepsilon_2$ आन्तरिक प्रतिरोध क्रमष: $r _1$ व $r _2$ है, श्रेणीक्रम मे संयोजित किये गये है। इस संयोजन को एक बाह्य प्रतिरोध $R$ जोडा गया है |प्रतिरोध $R$ में से प्रवाहित होने वाली धारा $I$ ज्ञात कीजिए।View Solution
- 2अपवाह वेग के आधार पर ओम के नियम का समीकरण $\overrightarrow{ J }=\sigma \overline{ E }$ प्राप्त कीजिए।View Solution
$($जहाँ संकेतों के सामान्य अर्थ हैं$)$