\(\mathrm{U}_{\mathrm{B}}=\mathrm{U}_{\mathrm{E}}\)
\(\frac{1}{2} \mathrm{Li}^{2}=\frac{\mathrm{q}^{2}}{2 \mathrm{C}}\)
where \(q\) is the charge on the capacitor when energy stored equally between the electric and magnetic fields.
\(\therefore \mathrm{q}^{2}=\mathrm{LCi}^{2}\) ........\((i)\)
Now maximum charge on the capacitor is \(Q\)
when maximum current \(i_{0}\) flows through the \(L-C\) circuit.
So, maximum energy stored in the electric and magnetic fields are
\(\left(\mathrm{U}_{\mathrm{E}}\right)_{\max }=\frac{\mathrm{Q}^{2}}{2 \mathrm{C}}\) and \(\left(\mathrm{U}_{\mathrm{B}}\right)_{\max }=\frac{1}{2} \mathrm{Li}_{0}^{2}\)
Given \(\left(\mathrm{U}_{\mathrm{B}}\right)=\frac{1}{2}\left(\mathrm{U}_{\mathrm{E}}\right)_{\max }\)
\(\frac{1}{2} \mathrm{Li}^{2}=\frac{1}{2} \frac{\mathrm{Q}^{2}}{2 \mathrm{C}}=\frac{\mathrm{Q}^{2}}{4 \mathrm{C}}\)
\(\frac{{{{\rm{q}}^2}}}{{2{\rm{C}}}} = \frac{{{{\rm{Q}}^2}}}{{4{\rm{C}}}}\) [from equation \((i)\)]
\(\therefore \) \(\mathrm{q}^{2}=\frac{\mathrm{Q}^{2}}{2}\)
\(\mathrm{q}=\frac{\mathrm{Q}}{\sqrt{2}}\)
Download our appand get started for free
Similar Questions
- 1$20\; V , 50$ ચક્ર/સેકન્ડ ના સંચાલક એ.સી. સ્રોત સાથે $12 \;\Omega$ નો અવરોધ અને $0.21\; H$ નો ઈન્ડકટર શ્રેણીમાં જોડેલ છે. વિદ્યુતપ્રવાહ અને વિદ્યુતસ્થિતિમાન વચ્ચે કળા ખૂણો કેટલો હશે?View Solution
- 2એક વૈકલ્પિક ઈએમએફનું પ્રતિરોધ $R$, કેપેસીિટન્સ $ C $ અને ઇન્ડક્ટન્સ $ L $ ના સમાંતર સંયોજનમાં લાગુ કરવામાં આવે છે. જો $ I_R $, $ I_L $, $ I_C $ અનુક્રમે $ R, \, L $ અને $ C$ દ્વારા પ્રવાહો હોય, તો પછી ચિત્ર જે યોગ્ય રીતે રજૂ કરે છે, $ I_R $, $ I_L $, $ I_C$ વચ્ચેના તબક્કાના સંબંધો અને સ્રોત ઇએમએફ $E$ દ્વારા આપવામાં આવે છેView Solution
- 3એક $LCR$ પરિપથ $110 \, \Omega$ અવરોધ અને $300$ રેડિયન/સે કોણીય આવૃત્તિવાળો $220\, V$ ઉદ્દગમ ધરાવે છે. જે માત્ર સંઘારક ને દૂર કરવામાં આવે તો પ્રવાહ, વોલ્ટેજ થી કળામાં $45^{\circ}$ પાછળ રહે છે અને જો માત્ર પ્રેરક દૂર કરવામાં આવે તો પ્રવાહ, વોલ્ટેજ થી $45^{\circ}$ આગળ રહે છે. પરિપથમાં પસાર થતાં પ્રવાહનું મૂલ્ય ...... $A$View Solution
- 4View Solution
જોડકાં જોડો.
પ્રવાહ $ r.m.s. $ મૂલ્ય
(1)${x_0 }\sin \omega \,t$ (i)$ x_0$
(2)${x_0}\sin \omega \,t\cos \omega \,t$ (ii)$\frac{{{x_0}}}{{\sqrt 2 }}$
(3)${x_0}\sin \omega \,t + {x_0}\cos \omega \,t$ (iii) $\frac{{{x_0}}}{{(2\sqrt 2 )}}$
- 5સર્કિટની અવરોધમાં $3\,ohm$ પ્રતિકાર અને $ 4\,ohm$ રિએક્શનનો સમાવેશ થાય છે. સર્કિટનો પાવર ફેક્ટર કેટલો થાય?View Solution
- 6$C$ કેપેસિટન્સ ઘરાવતા કેપેસિટરને $V_1$ વિદ્યુતસ્થિતિમાનથી વિદ્યુતભારીત કરેલ છે. હવે, આ કેપેસિટરને $L$ ઇન્ડકટન્સ ધરાવતા આદર્શ ઇન્ડકટર સાથે જોડવામાં આવે છે. જયારે કેપેસિટર પરનો વિદ્યુતસ્થિતિમાન ઘટીને $V_2$ થાય, ત્યારે ઇન્ડકટરમાંથી વહેતો વિદ્યુતપ્રવાહ કેટલો થાય?View Solution
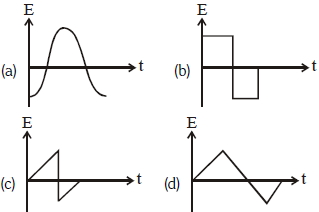
- 7ચાર પ્રકારના જનરેટર માટે બદલાતા $EMF$ નો સમય સાથેનો આલેખ નીચે આપેલ છે. નીચે પૈકી કયો આલેખ $AC$ કહેવાય?View Solution
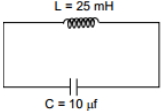
- 8$t =0$ સમયે કેપેસિટરમાં મહતમ ઊર્જા છે,તો કેટલા સમય પછી પરિપથમાં મહતમ પ્રવાહ થાય.View Solution
- 9એક $LCR$ પરિપથ, સંધારક $C$, પ્રેરક $L$ અને અવરોધ $R$ માટે અનુનાદ સ્થિતિમાં છે. હવે બાકીના પ્રાચલો બદલ્યા સિવાય અવરોધનું મૂલ્ય અડધું કરવામાં આવે છે. હાલમાં મળતો અનુનાદનો કંપવિસ્તાર હવે. . . . . . . .View Solution
- 10સમાંતર પ્લેટ સંઘારકમાં વાહક પ્રવાહનું $rms$ મૂલ્ય $6.9\,\mu\,A$ છે. જે સંઘારકકન $600\,rad / s$, ની કોણીય આવૃત્તિ ધરાવતા $230\,V$ ના $ac$ ઉદગમ સાથે જોડવામાં આવે તો સંઘારકની સંઘારકતા $....\,pF$ હશે.View Solution
