Charge located at the origin, \(q=8 \,mC =8 \times 10^{-3} \,C\)
Magnitude of a small charge, which is taken from a point \(P\) to point \(R\) to point \(Q, \;\;q_{1}=-2 \times 10^{-9} \,C\)
All the points are represented in the given figure.
Point \(P\) is at a distance, \(d_{1}=3 \,cm ,\) from the origin along \(z\) -axis. Point \(Q\) is at a distance, \(d _{2}=4 \,cm ,\) from the origin along \(y\) -axis.
Potential at point \(P, \quad V_{1}=\frac{q}{4 \pi \epsilon_{0} \times d_{1}}\)
Potential at point \(Q\), \(\quad V_{2}=\frac{q}{4 \pi \epsilon_{0} d_{2}}\)
Work done \((W)\) by the electrostatic force is independent of the path. \(\therefore W=q_{1}\left[V_{2}-V_{1}\right]\)
\(=q_{1}\left[\frac{q}{4 \pi \epsilon_{0} d_{2}}-\frac{q}{4 \pi \epsilon_{0} d_{1}}\right]\)
\(=\frac{q q_{1}}{4 \pi \epsilon_{0}}\left[\frac{1}{d_{2}}-\frac{1}{d_{1}}\right]\)
Where, \(\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \,N\, m ^{2} \,C ^{-2}\)
\(\therefore W=9 \times 10^{9} \times 8 \times 10^{-3} \times\left(-2 \times 10^{-9}\right)\left[\frac{1}{0.04}-\frac{1}{0.03}\right]\)
\(=-144 \times 10^{-3} \times\left(\frac{-25}{3}\right)\)
\(=1.27 \,J\)
Therefore, work done during the process is \(1.27 \;J\)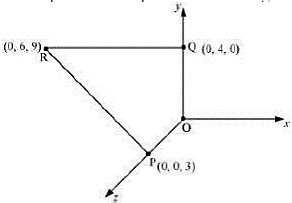
Download our appand get started for free
Similar Questions
- 1એક સમાંતર પ્લેટો ધરાવતા સંધારકમાં પ્લેટનું ક્ષેત્રફળ $40\,cm ^2$ અને તેમની વચ્યેનું અંતર $2\,mm$ છે. પ્લેટો વચ્યેના વિસ્તારમાં $1\,mm$ જાડાઈ અને $5$ જેટલો ડાઈઈલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકવામાં આવે છે. તંત્રની સંધારકતા $...........$ થશે.View Solution
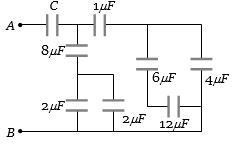
- 2$A$ અને $B$ વચ્ચે સમતુલ્ય કેપેસિટન્સ $1 \,\mu F$ છે.તો $C$ નું મૂલ્ય કેટલું હશે?View Solution
- 3અંનત સંખ્યાઓના કેપેસિટરોનું કેપેસિટન્સ અનુક્રમે $C, 4\ C, 16\ C$ …..$\infty$ તેઓને શ્રેણીમાં જોડેલા હોય ત્યારે તેઓનો પરિણામી કેપસિટન્સ કેટલા ........$C$ હશે ?View Solution
- 4$1\ g$ અને $10^{-8} \,C$ વિદ્યુતભાર વાળો એક બોલ બિંદુ $A \,(V_A = 600 \,V)$ થી જેનું સ્થિતિમાન શૂન્ય હોય તેવા બિંદુ $B$ તરફ ગતિ કરે છે. $B$ બિંદુ આગળ બોલનો વેગ $20\, cm\, s^{-1}$ છે. બિંદુ $A$ આગળ બોલનો વેગ.......$cm/s$ માં શોધો.View Solution
- 5$5\,mm$ અને $10\,mm$ ત્રિજ્યાઓ ધરાવતા અને નિયમિત વિદ્યુતભારીત બે નળાકારીય સુવાહકો $A$ અને $B$ ને $2\,cm$ અંતરે છૂટા પાડેલા છે. જો ગોળાઓને એક સુવાહક તાર વડે જોડવામાં આવે તો, સંતુલન અવસ્થામાં ગોળા $A$ અને $B$ ની સપાટી ઉપર વિદ્યુતક્ષેત્રનાં :મૂલ્યોનો ગુણોત્તર $.......$ થશે.View Solution
- 6પ્લેટોની વચ્ચે $K$ ડાય-ઈલેકટ્રીક અચળાંક ધરાવતા ડાય ઈલેકટ્રીક સાથે એક સમાંતર પ્લેટ સંગ્રાહકની કેપેસિટી $C$ અને $A$ ને $V$ વોલ્ટ સ્થિતિમાન સુધી ચાર્જ કરેલ છે. પ્લેટો વચ્ચે ડાઈ ઈલેકટ્રીન સ્લેબને ધીમે ધીમે દૂર કરવામાં આવે છે અને ત્યારબાદ ફરી દાખલ કરવામાં આવે છે. આ પ્રક્રિયા તંત્ર દ્વારા થતું ચોખ્ખું કાર્ય.....View Solution
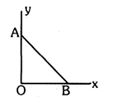
- 7આ આલેખ પરથીએક બિંદુવત વિદ્યુતભાર $+q$ ને ઉગમબિંદુ આગળ મૂકેલો છે. બીજા બિંદુવત વિદ્યુતભાર $-Q$ ને સુરેખ પથ $AB$ પર બિંદુ $A$ ના યામ $(0, a)$ ન થી બિંદુ $B$ ના યામ $(a, 0)$ ન સુધી લઈ જતાં થતુ કાર્ય ....... છે.View Solution
- 8$q,-2 q$ અને $q$ જેટલો ચાર્જ ધરાવતા ત્રણ કણો એેક રેખા પર $(-a, 0),(0,0)$ અને $(a, 0)$ પર રાખેલા છે, તો $P(r, 0)$ કે આ $r \gg > $ હોય તેવા બિંદુએ મળતાં સ્થિતિમાનનું સુત્ર શું ગણાય?View Solution
- 9શ્રેણીમાંના બે કેપેસિટર $C_1 = 2 \,\mu F$ અને $C_2 = 6 \,\mu F$ ને ત્રીજા કેપેસિટર સાથે સમાંતરમાં જોડવામાં આવે છે. આ ગોઠવણીને ત્યારબાદ $C_3 = 4 \,\mu F$ ની બેટરી સાથે જોડવામાં આવે છે. કેપેસિટરોને વિદ્યુતભારીત કરવા માટે બેટરી દ્વારા કેટલી ઊર્જા આપવામાં આવે છે.View Solution
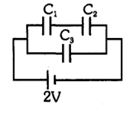
- 10$K$ જેટલો ડાયઈલેકિટ્રક અચળાંક ધરાવતા દ્રવ્યના બનેલા એક યોસલાને, સમાંતર પ્લટો ધરાવતા સંધારકની પ્લેટો જેટલું જ ક્ષેત્રફળ છે, અને તેની જાડાઈ $\frac{3}{4}$ d, જેટલી છે, જયાં $d$ એ પ્લેટો વચ્ચેનું અંતર છે. જ્યારે પ્લેટોની વચ્ચે યોસલાને દાખલ કરવામાં આવશે ત્યારે સંધારકતા કેટલી થશે ? ( $C _0=$ જયારે સંધારકની પ્લેટો વચ્યેનું માધ્યમ હવા હોય, ત્યાર ની સંધારકતા.)View Solution
