એક સમાંતર પ્લેટો ધરાવતા સંધારકમાં પ્લેટનું ક્ષેત્રફળ $40\,cm ^2$ અને તેમની વચ્યેનું અંતર $2\,mm$ છે. પ્લેટો વચ્યેના વિસ્તારમાં $1\,mm$ જાડાઈ અને $5$ જેટલો ડાઈઈલેકિટ્રક અચળાંક ધરાવતો અવાહક મૂકવામાં આવે છે. તંત્રની સંધારકતા $...........$ થશે.
JEE MAIN 2023, Medium
c
This can be seen as two capacitors in series combination so
This can be seen as two capacitors in series combination so
\(\frac{1}{C_{e q}}=\frac{1}{C_1}+\frac{1}{C_2}\)
\(=\frac{1}{\frac{K \in_0 A}{t}}+\frac{1}{\frac{\epsilon_0 A}{d-t}}\)
\(=\frac{ t }{ K \in_0 A }+\frac{ d - t }{\epsilon_0 A }\)
\(=\frac{1 \times 10^{-3}}{5 \epsilon_0 \times 40 \times 10^{-4}}+\frac{1 \times 10^{-3}}{\epsilon_0 40 \times 10^{-4}}\)
\(\frac{1}{ C _{ eq }}=\frac{1}{20 \epsilon_0}+\frac{1}{4 \epsilon_0}\)
\(C _{ eq }=\frac{20 \times 4 \epsilon_0}{24}=\frac{10 \epsilon_0}{3} F\)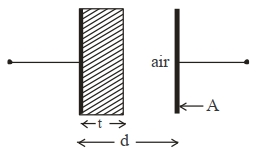
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$a$ બાજુવાળા ચોરસના શિરોબિંદુ પર $Q$ વિજભાર મૂકવામાં આવે છે. ચોરસના કેન્દ્રથી $-Q$ વિજભારને અનંત અંતરે લઈ જવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 2View Solutionવિદ્યુતભારની ધ્રુવીભવનનો સિધ્ધાંત કોણે સાબિત કર્યો હતો?
- 3દસ વિદ્યુતભારને $R$ ત્રિજ્યાના વર્તુળ પર સમાન કોણીય અંતરે મૂકેલા છે. વિધુતભાર $1,3,5,7,9$ પાસે $(+q)$ અને વિધુતભાર $2,4,6,8,10$ પાસે $(-q)$ વિધુતભાર છે તો વર્તુળના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર અને વિદ્યુતસ્થિતિમાનView Solution
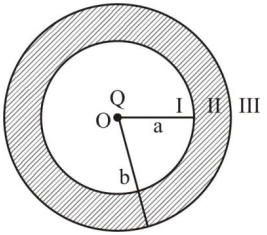
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે, આંતર ત્રિજ્યા $a$ અને બાહ્ય ત્રિજ્યા $b$ વાળા ગોળીય વાહક કવચના કેન્દ્રમાં બિંદુવત વીજભાર $Q$ મૂકેલ છે. વીજભાર $Q$ ને લીધે ત્રણ ભિન્ન વિસ્તાર $I, II$ અને $III$ માં વીજ ક્ષેત્ર $..............$ હશે. $\text { (I :r } r < a \text {, II : } a < r < b, \text { III: } r > b \text { ) }$View Solution
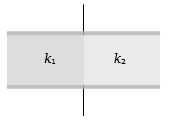
- 5બે ડાઈઇલેક્ટ્રીક ભરેલા કેપેસીટરને આકૃતિમાં દર્શાવ્યા મુજબ આપેલ છે જ્યાં પ્લેટનું ક્ષેત્રફળ $A\;metr{e^2}$ અને બે ફ્લૅટ વચ્ચેનું અંતર $t$ $metre$ હોય તથા ડાઈઇલેક્ટ્રીક અચળાંક અનુક્રમે ${k_1}$ અને ${k_2}$ હોય તો સમતુલ્ય કેપેસીટન્સ મેળવોView Solution
- 6$R$ ત્રિજયાની બે રીંગને $R$ અંતરે સમઅક્ષિય મૂકેલ છે,તેનાં પર વિદ્યુતભાર $Q_1$ અને $Q_2$ છે.તો $q$ વિદ્યુતભારને એક રીંગના કેન્દ્રથી બીજી રીંગના કેન્દ્ર સુધી લઇ જવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 7$C$ કેપેસિટન્સવાળા એક સમાંતર પ્લેટ કેપેસિટરને બેટરી સાથે જોડી $V$ સ્થિતિમાને વિદ્યુતભારિત કરવામાં આવે છે. બીજા $2C$ કેપેસિટન્સ ધરાવતા કેપેસિટરને બીજી બેટરી સાથે જોડી $2V$ સ્થિતિમાને વિદ્યુતભારીત કરવામાં આવે છે. આ બેટરીઓને દૂર કર્યા બાદ અને કેપેસિટરોને સમાંતરમાં એવી રીતે જોડવામાં આવે છે કે જેથી એકની ધન પ્લેટ બીજાની ઋણ પ્લેટ સાથે જોડેલી હોય, તો તંત્રની અંતિમ ઉર્જા ગણો.View Solution
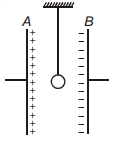
- 8View Solutionઆકૃતિમાં દર્શાવ્યા પ્રમાણે સમાંતર પૃષ્ઠ કેપેસિટરના પૃષ્ઠોની વચ્ચે અવાહક તાર વડે એક નાનો સુવાહક ગોળો લટકાવવામાં આવેલ છે. ગોળા પર લાગતું કુલ બળ કઈ દિશામાં છે?
- 9કેપેસિટરને $V$ વૉલ્ટની બેટરી સાથે જોડેલ છે,તેના ડાઇઇલેક્ટ્રીક અચળાંક $k$ ધરાવતું માધ્યમ કેપેસીટરમાં દાખલ કરતાં કેપેસિટરમાં દાખલ કરતા કેપેસિટર પર નવો વિદ્યુતભાર .....View Solution
- 10બે સમાન કેપેસિટરને શ્રેણીમાં જોડીને $100\,V$ ની બેટરી સાથે જોડવામાં આવે છે.તેમાંથી બીજા કેપેસિટરમાં ડાઇઇલેકિટ્રક અચળાંક $4$ ભરવાથી કેપેસિટરના વોલ્ટેજ કેટલા થાય?View Solution
