એક અનંત લંબાઈનો રેખીય વિદ્યુતભાર $2 \,cm$ અંતરે $9 \times 10^4 \;N/C$ વિદ્યુતક્ષેત્ર ઉત્પન્ન કરે છે. રેખીય વિદ્યુતભાર ઘનતા ($\mu C / m$ માં) ગણો.
Easy
d
Electric field produced by the infinite line charges at a distance d having linear charge density
Electric field produced by the infinite line charges at a distance d having linear charge density
\(\lambda\) is given by the relation,
\(E=\frac{\lambda}{2 \pi \varepsilon_{0} d} \Rightarrow \lambda=2 \pi \varepsilon_{0} d E\)
Where, \(d =2 \,cm =0.02 \,m , E =9 \times 10^{4} \,N / C\)
\(\varepsilon_{0}=\) Permittivity of free space and \(\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} Nm ^{2} C ^{-2}\)
Therefore, \(\lambda=\frac{0.02 \times 9 \times 10^{4}}{2 \times 9 \times 10^{9}}=10\, \mu \,C / m\)
Therefore, the linear charge density is \(10\; \mu \,C / m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઋણ વિદ્યુતભાર ધરાવતા ટીપાને ગુરૂત્વાકર્ષણની વિરૂધ્ધ શિરોલંબ $100\ V m^{-1}$ જેટલુ વિદ્યુતક્ષેત્ર આપીને પડતા અટકાવવામાં આવે છે જો ટીપાંનું વજન $1.6 \times 10^{-3}\ g$ હોય તો ટીપામાં સમાયેલ ઇલેક્ટ્રોનની સંખ્યા....View Solution
- 2વિદ્યુતક્ષેત્ર શોધવા ગાઉસનો નિયમ $|\overrightarrow{\mathrm{E}}|=\frac{q_{\mathrm{enc}}}{\varepsilon_{0}|\mathrm{A}|}$ વાપરવામાં આવે છે.જ્યાં $\varepsilon_{0}$ શૂન્યાવકાશની પરમિટિવિટી, $A$ ગાઉસીયન સપાટીનું ક્ષેત્રફળ અને $q_{enc}$ એ ગાઉસીયન સપાટીની અંદર રહેલ વિજભાર છે.ઉપરનું સૂત્ર ક્યારે વાપરવામાં આવે છે?View Solution
- 3$1$ $\mu$$C$ અને $5$ $\mu$$C$ ના બે વિદ્યુતભારો $4\, cm$ દૂર આવેલા છે. બંને વિદ્યુતભારો એકબીજા પર લાગતા બળનો ગુણોત્તર....... હશે.View Solution
- 4ગોળા અંદર વિદ્યુતભાર $+ 2 × 10^{-6}\ C, -5 × 10^{-6}\ C, -3 × 10^{-6}\ C, +6 × 10^{-6}\ C$ હોય,તો ગોળામાંથી કેટલું ફલ્કસ પસાર થાય?View Solution
- 5બે ઈલેક્ટ્રોનને $'2d'$ અંતરે જડિત રાખવામાં આવ્યા છે. એક ત્રીજા વિદ્યુતભાર પ્રોટોન કે જે મધ્યબિંદુએ રાખી તેને $x (x < < d)$ જેટલા ખૂબ નાના અંતરે બે જડીત વિદ્યુતભારોને જોડતી રેખાને લંબ ખસેડવામાં આવે છે. પ્રોટોન ......... કોણીય આવૃત્તિ સાથે સરળ આવર્ત ગતિ કરે છે. $(m \, =$ વિધુતભારિત કણનું દળ$)$View Solution
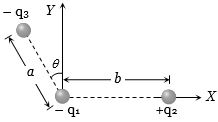
- 6ત્રણ વિદ્યુતભારો $ - {q_1},\,\, + {q_2}$ અને $ - {q_3}$ ને આકૃતિમાં બતાવ્યા પ્રમાણે મૂકવામાં આવ્યા છે. $- q_1$ વિદ્યુતભાર પર લાગતા બળનો $X$ ઘટક કોના સપ્રમાણમાં હોય?View Solution
- 7હવામાં $r$ અંતરે રહેલા બે વિદ્યુતભાર પર લાગતું બળ $F$ છે.હવે $k$ ડાઇઇલેકિટ્રક ધરાવતા માધ્યમ મૂકવાથી લાગતું બળ કેટલું થાય?View Solution
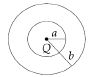
- 8ત્રિજયા $‘a’$ અને ત્રિજયાા $‘b’$ ધરાવતા બે સમકેન્દ્રિય ગોળા ( જુઓ ચિત્ર ) ની વચ્ચેના ભાગમાં વિદ્યુત ઘનતા $\rho = \frac{A}{r}$ છે.જયાં $A$ અચળાંક છે અને કેન્દ્ર થી અંતર $r$ છે. ગોળાઓના કેન્દ્ર પર બિંદુવત વિદ્યુતભાર $Q$ છે.ગોળાઓનના વચ્ચેના ભાગમાં વિદ્યુતક્ષેત્ર અચળ રહે તે માટેના $A$ નું મૂલ્ય છે.View Solution
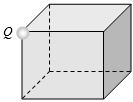
- 9સમઘનના ખૂણા પર $Q$ વિદ્યુતભાર મૂકતાં સમઘનની એક બાજુમાંથી કેટલું ફલ્કસ પસાર થાય?View Solution
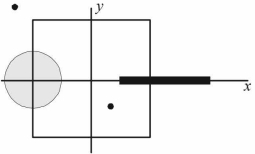
- 10$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution