ન્યુટન ના સૂત્ર પરથી \(({{\vec v}_2}-{{\vec v}_1})=e({{\vec u}_2}-{{\vec u}_2})\)
\({\text{v}}\,\, = \,\,\sqrt {{\text{2gh}}} \) અહી , \({{\vec v}_2}\, = \,\,0,\,\,{{\vec u}_2}\, = \,\,0\) (સ્થિર સ્થિતિ આગળની સપાટી )
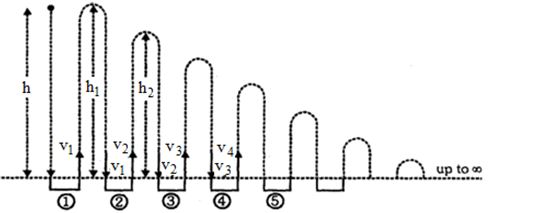
\('n'\) વાર પાછો ફર્યા પછી બોલ વડે હાંસલ થતી ઊચાઇ :
\(V_1=ev⇒\sqrt {{\text{2gh}}}_1=e\sqrt {{\text{2gh}}}⇒h_1=e^2hv_2=e^2v\)
\(\sqrt {{\text{2gh}}}_2=e^2\sqrt {{\text{2gh}}}⇒h_2=e^4h\)
તેવી જ રીતે \(,h_n=e^{2n}h\)
\(n\) વાર પાછો ફરવા માટે લાગતો સમય
\({h_1}\, = \,\,{e^2}h\,\,\,\, \Rightarrow \,\,\,\frac{1}{2}gt_1^2\,\, = \,\,{e^2}\frac{1}{2}\,\,g{t^2}\,\,\, \Rightarrow \,\,\,t_1^2\,\, = \,\,{e^2}{t^2}\,\,\,\, \Rightarrow \,\,\,{t_1}\, = \,\,et\,\,\,{t_1}\, = \,\,e\,\sqrt {\frac{{2h}}{g}} \,\,\,\,...........(i)\)
\({h_2}\, = \,\,{e^4}h\,\,\,\,\, \Rightarrow \,\,\,\,\frac{1}{2}g{t_2}^2\,\, = \,\,{e^4}(\frac{1}{2}\,\,g{t^2})\,\,\,\, \Rightarrow \,\,\,t_2^2\, = \,\,{e^4}{t^2}\,\,\,\, \Rightarrow \,\,\,{t_2}\, = \,\,{e^2}t\,\,\, \Rightarrow \,\,{t_2}\, = \,\,{e^2}\,\sqrt {\frac{{2h}}{g}} \,\,\,.........(ii)\)
તેવી જ રીતે \(,\,\,\,{{\text{t}}_{\text{n}}}\, = \,\,{e^n}\,\sqrt {\frac{{2h}}{g}} \,\,\,\,\therefore \,\,\,\,\,{t_n}\, = \,\,{e^n}t\)
Download our appand get started for free
Similar Questions
- 1$50 g $ ની ગોળી $10 m/s $ ના વેગથી $950 gm$ ના સ્થિર બ્લોકમાં ધૂસીને સ્થિર થઇ જાય છે.તો તંત્ર કેટલા ................. $\%$ ગતિઊર્જા ગુમાવશે?View Solution
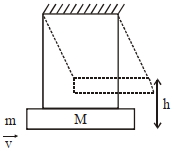
- 2$M=5.99 \,kg$ દળ ધરાવતું એક મોટું ચોસલું બે દળરહિત દોરીઓ વડે લટકાવવામાં આવેલ છે. $m=10\, g$ દળ ધરાવતી ગોળીને ચોસલાંમાં ફાયર (ફોડવામાં) કરવામાં આવે છે અને તે તેમાં ઘૂસી જાય છે. (ચોસલું$+$ગોળી) પછી ઉપર તરફ ગતિ કરે છે, આ દોલક (ચોસલું$+$ગોળી) તેમની માપના અંત્ય બિંદુ આગળ ક્ષણભાર સ્થિર થાય તે પહેલા તેમના દ્રવ્યમાન કેન્દ્ર શિરોલંબ દિશામાં $h=9.8\, cm$ ઊંચાઈએ પહોંચે છે. સંધાત પહેલા તરત જ ગોળીની ઝડપ ..... હશો. ($g =9.8\, ms ^{-2}$ લો.) ($m/s$ માં)View Solution
- 3પરમાણુના બે અણુઓ વચ્ચેની સ્થિતિઊર્જા $U(x) = \frac{a}{{{x^{12}}}} - \frac{b}{{{x^6}}}$ દ્વારા આપવામાં આવે છે; જ્યાં $a$ અને $b$ એ ધન અચળાંકો છે અને $x$ એ અણુઓ વચ્ચેનું અંતર છે. અણુ સ્થાયી સંતુલનમાં હશે જ્યારે .......View Solution
- 4$x -$ દિશામાં $2v$ જેટલી ઝડપથી ગતિ કરતો અને $m$ દળ ધરાવતો કણ $y-$ દિશામાં $v$ જેટલી ઝડપથી ગતિ કરતા બીજા $2m$ દળ ધરાવતા કણ સાથે અથડાય છે.આ અથડામણ જો સંપૂર્ણ અસ્થિતિસ્થાપક હોય,તો અથડામણ દરમિયાન ઊર્જામાં થતો પ્રત્યાશિત ફેરફાર ..................... $\%$ ની નજીક ( જેટલો ) હશે.View Solution
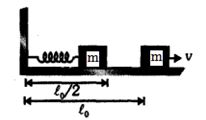
- 5$m$ દળનો એક ટુકડો $k$ સ્પ્રિંગ અચળાંકવાળી એક સ્પ્રિંગ કે જેનો એક છેડો દિવાલ સાથે જોડાયેલ છે તેની વિરૂદ્ધમાં ધકેલાય છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ટુકડો ઘર્ષણરહિત ટેબલ પર સરકે છે. સ્પ્રિંગની પ્રાકૃતિક લંબાઈ $l_0$ છે અને જ્યારે ટુકડો મુક્ત થાય છે ત્યારે તે તેની પ્રાકૃતિક લંબાઈની અડધી લંબાઈ જેટલી સંકોચાય છે તો ટુકડાનો અંતિમ વેગ કેટલો હશે ?View Solution
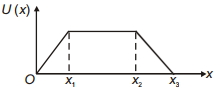
- 6એક તંત્રની સ્થિતિઊર્જા $U$ માં થતો ફેરાફાર એ આકૃતિમાં દર્શાવ્યા મુજબ છે. તો તંત્ર પર લાગતું બળ એ શ્રેષ્ઠ રીતે ક્યાં આલેખ મુજબ દર્શાવી શકાય?View Solution
- 7એક $m $ દળનો પદાર્થ અચળ બળ $F$ ની અસર હેઠળ પ્રારંભિક સ્થિર સ્થિતિએથી $t$ સમયમાં $v m/sec$ વેગ હાંસલ કરે છે દળનો જરૂરી પાવર કટેલો હશે ?View Solution
- 8એક સમક્ષિતિજ સમતલ પર $2m$ ત્રિજ્યાવાળી ગોળીય તકતી ગોઠવેલી છે. જેના અંતર્ગોળ પૃષ્ઠ પર $1 g$ દળનો એક કણ દોલીત ગતિ કરે છે. જો કણની ગતિની શરૂઆત સમક્ષિતિજ સમતલથી $1 cm $ ઉંચાઈએ આવેલી તકતી પરના એક બિંદુથી થાય છે અને ઘર્ષણ ગુણાંક $0.01$ છે. કણ સ્થિર સ્થિતિએ રહેલ અંતર્ગોળ પૃષ્ઠના નીચેના ભાગે આવે તે પહેલા તેણે કુલ ........ $m$ અંતર કાપ્યું હશે.View Solution
- 9એક $m_1$ દળનો કણ $v_1 $ વેગ સાથે ગતિ કરે છે અને બીજો $m_2$ દળનો કણ $V_2$ વેગ સાથે ગતિ કરે છે. તે બંનેનું વેગમાન સમાન છે પરંતુ તેમની જુદી જુદી ગતિ ઊર્જા અનુક્રમે $E_1$ અને $E_2$ છે. જો $m_1$ > $m_2$ હોય તો.......View Solution
- 10બે સમાન લાદીના ઢેફાઓને બાજુ બાજુએથી બે લાંબી દોરી વડે લટકાવેલા છે. એક બાજુ દોરવામાં આવે છે કે જેથી તેનું ગુરૂત્વકેન્દ્ર $h $ શિરોલંબ અંતર વધે છે. તેને મુક્ત કરવામાં આવે છે અને ત્યારે તે બીજા એક સાથે અસ્થિતિસ્થાપક રીતે સંઘાત પામે છે. તો આ સંયોજનના ગુરૂત્વકેન્દ્રથી વધેલા શિરોલંબ અંતર કેટલું હશે ?View Solution
