એક બોલને ઉપર તરફ અમુક વેગથી ફેંકવામાં આવે છે કે જેથી તે મહત્તમ $h$ ઊંચાઈ સુધી પહોચે છે. અનુક્રમે ઉપર જતી અને નીચે આવતી વખતે જ્યારે બોલ $\frac{h}{3}$ ઉંચાઈએ હોય, ત્યારે સમયોનો ગુણોત્તર શોધો.
JEE MAIN 2022,JEE MAIN 2021, Diffcult
b
Max. Height \(= h =\frac{ u ^{2}}{2 g }\)
Max. Height \(= h =\frac{ u ^{2}}{2 g }\)
\(\Rightarrow u =\sqrt{2 gh }\)
\(S =u t+\frac{1}{2} a t^{2}\)
\(\frac{ h }{3}=\sqrt{2 gh } t +\frac{1}{2}(- g ) t ^{2}\)
\(\frac{ gt ^{2}}{2}-\sqrt{2 ght }+\frac{ h }{3}=0 \quad\) (Roots are \(t _{1} \& t _{2}\) )
\(\frac{t_{2}}{t_{1}}=\frac{\sqrt{2 g h}+\sqrt{2 g h-4 \times \frac{g}{2} \times \frac{h}{3}}}{\sqrt{2 g h}-\sqrt{2 g h-4 \times \frac{g}{2} \times \frac{h}{3}}}=\frac{\sqrt{2 g h}+\sqrt{\frac{4 g h}{3}}}{\sqrt{2 g h}-\sqrt{\frac{4 g h}{3}}}=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\)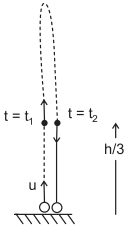
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેનામાંથી કયો આલેખ એક પરિમાણિક ગતિ દર્શાવતો નથી?
- 2ચોક્કસ ઊંચાઈ $h$ ($h$ ખૂબ મોટી છે) થી એક પદાર્થને મુક્ત પતન કરવામાં આવે છે અને બીજા પદાર્થને $5 \,m / s$ ના વેગ સાથે નીચેની તરફ ફેકવામાં આવે છે. $3 \,s$ પછી બે પદાર્થની ઊંચાઈમાં ........... $m$ તફાવત હશે ?View Solution
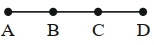
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે પદાર્થ અનુક્રમે $AB, BC$ અને $CD$ રેખાખંડ પર $v_1, v_2$ અને $v_3$ ઝડપથી ગતિ કરે છે. જ્યાં $AB = BC$ અને $AD =3 AB$, તો પદાર્થની સરેરાશ ઝડપ કેટલી હશે?View Solution
- 4$\mathrm{Y}-\mathrm{Z}$ સમતલમાં ગતિ કરતી એક કીડીનું સ્થાન ( $\mathrm{S}$ મીટરમાં ) $\mathrm{S}=2 \mathrm{t}^2 \hat{j}+5 \hat{k}$ (જ્યાં $\mathrm{t}$ સેકંડમાં છે) વડે દર્શાવવામાં આવે છે. $t=1 \mathrm{~s}$ વખતે કીડીના વેગના મૂલ્ય અને દિશા _______થશે.View Solution
- 5એક નદી પર એક સમક્ષિતિજ પુલ બાંધવામાં આવ્યો છે. પુલ પર ઊભેલ વિદ્યાર્થી એક નાનો દડો (બૉલ) $4\,m s ^{-1}$ વેગથી શિરોલંબ ઉર્ધ્વ દિશામાં ફેંકે છે. દડો $4\,s$ બાદ પાણીની સપાટી પર પછડાય છે. પાણીની સપાટીથી પુલની ઊંચાઈ $.......\,m$ છે.$\left( g =10 m s ^{-2}\right.)$ લો.View Solution
- 6એક કણ સીધી રેખા $OX$ પર ગતિ કરે છે. $t ($સેકન્ડમાં$)$ સમયે કણના $O$ થી અંતર $x$ (મીટરમાં) એ $x =40+12 t - t ^{3}$ વડે આપવામાં આવે છે. આ કણ સ્થિર થશે તે પહેલાં કેટલા$.........m$ અંતર કાપશે?View Solution
- 7એક વિમાન $400 \,m$ ઉત્તરમાં અને $300 \,m$ દક્ષિણ માં અને ત્યારબાદ $1200 \,m$ ઉપર તરફ ઊડે છે, તો તેણે કરેલું ચોખ્ખું સ્થાનાંતર કેટલા ............$m$ થાય?View Solution
- 8એક પદાથૅ સ્થિર સ્થિતિમાંથી $8\,m/{\sec ^2},$ ગતિની શરૂઆત કરે છે.તેને $5^{th}\ sec$ માં કેટલા ..........$metres$ અંતર કાપશે?View Solution
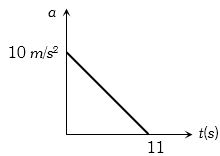
- 9સ્થિર સ્થિતિમાંથી ગતિ કરતાં પદાર્થનો પ્રવેગ વિરુધ્ધ સમયનો આલેખ આપેલ છે.તો પદાર્થની મહત્તમ ઝડપ કેટલી ......$m/s$ થશે?View Solution
- 10$44.1 \,m$ ઊંચાઇ ધરાવતા એક પુલ ઉપરથી પથ્થરને મુકત કરવામાં આવે છે.$1 \,sec$ પછી બીજા પદાર્થને ફેંકવામાં આવે છે.બંને પદાર્થ પાણીમાં એક સાથે પડે છે.તો બીજા પદાર્થને કેટલા......$m/s$ વેગથી ફેંકયો હશે?View Solution
