એક ફોટો-ડાયોડના પદાર્થનો બૅન્ડગૅપ $2.0 $ $eV$ છે. આ પદાર્થ ઓછામાં ઓછી કઈ આવૃત્તિવાળું વિકિરણનું શોષણ કરી શકે ?
Medium
d
\({E_g} = \,\,2\,eV\,\, = \,\,2\,\, \times \,\,1.6\,\, \times \,\,{10^{ - 19}}\,\, = \,\,3.2\,\, \times \,\,{10^{ - 19}}\,J\)
\({E_g} = \,\,2\,eV\,\, = \,\,2\,\, \times \,\,1.6\,\, \times \,\,{10^{ - 19}}\,\, = \,\,3.2\,\, \times \,\,{10^{ - 19}}\,J\)
\({E_g} = \,\,h{f}\)
\(\therefore \,{f}\,\, = \,\frac{{{E_g}}}{h}\,\, = \,\,\frac{{3.2\,\, \times \,\,{{10}^{ - 19}}}}{{6.62\,\, \times \,\,{{10}^{ - 34}}}}\,\,\,\,\,\,\therefore \,\,{f}\,\, = \,\,0.48\,\, \times \,\,{10^{15}}\,\, \approx \,\,\,5\,\, \times \,\,{10^{14}}\,Hz\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
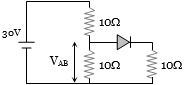
- 1આપેલ પરિપથમાં $V_{AB}$ કેટલા ......$V$ થાય?View Solution
- 2View Solutionનીચા તાપમાને શેમાં વેલેન્સ બેન્ડ અને કન્ડકટન્સ બેન્ડ ઓવરલેપ હોય છે?
- 3View Solutionનીચેનામાંથી ક્યો ગેટ યુનિવર્સલ ગેટ છે
- 4View Solutionનીચે દર્શાવેલ પરિપથોમાંથી કયા પરિપથમાં ડાયોડ રિવર્સ બાયસમાં છે ?
- 5નીચે દર્શાવેલ ટ્રુથ ટેબલ કયા લોજિક પરિપથ દર્શાવે છે?View Solution
$A\,\, 0\,\, 1\,\, 0\,\, 1$
$B \,\,0\,\, 0\,\, 1 \,\,1$
$y \,\,1\,\, 0\,\, 0\,\, 0$
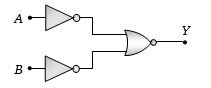
- 6View Solutionઆપેલ પરિપથ કયો ગેટ બને?
- 7View Solutionનીચે દર્શાવેલ આકૃત્તિઓમાં, સોલાર સેલની લાક્ષણિાક્તા ............. દર્શાવે છે.
- 8$N - P - N$ ટ્રાન્ઝિસ્ટર ઍમ્પ્લિફાયરમાં કલેક્ટર પ્રવાહ $9 mA$ છે. જો ઍમિટરમાંથી $90\% $ ઇલેકટ્રૉન કલેક્ટરમાં પહોંચતા હોય, તો ...View Solution
- 9એક એમ્એપ્મ્પ્લલીફાયર પરિપથમાં એક ટ્રાન્ઝિસ્ટરને કોમન એમીટર સંરચનામાં જોડવા માં આવેલ છે. જ્યારે બેઝ-એમીટર વોલ્ટેજમા $10\, mV$ નું સિગ્નલ ઉમેરવામાં આવે છે તો બેઝ-પ્રવાહ $10 \,\mu A$ જેટલો બદલાય છે અને કલેકટર-પ્રવાહ $1.5 mA$ જેટલો બદલાય છે. ભાર અવરોધ $5 \,k \Omega$ છે. ટ્રાન્ઝિસ્ટરનની વોલ્ટેજ લબ્ધિ........ હશેView Solution
- 10$Ga-As-P$ અર્ધવાહકમાંથી બનાવેલ $LED$ ની બેન્ડગેપ ઊર્જા $1.9\, eV$ હોય તો તેમાથી ઉત્પન્ન થતી તરંગલંબાઈ .........View Solution
