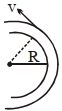
એક કાર $R$ ત્રિજયાના વક્ર માર્ગ પર ગતિ કરે છે. માર્ગનો ઢાળ $\theta $ કોણ જેટલો છે. કારના ટાયર અને માર્ગ વચ્ચેનો ઘર્ષણાંક ${\mu _s}$ છે. આ માર્ગ પર મહત્તમ સલામત વેગ કેટલો હશે?
NEET 2016, Diffcult
a
\(\begin{array}{l}
For\,vertical\,equilibrium\,on\,the\,road,\\
N\cos \theta = mg + f\sin \theta \\
mg = N\cos \theta - f\sin \theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
Centripetal\,force\,for\,safe\,turning\,,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,N\sin \theta + f\cos \theta = \frac{{m{v^2}}}{R}\,\,\,\,\,\,...\left( {ii} \right)\\
From\,eqns.\,\left( i \right)\,and\,\left( {ii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\frac{{{v^2}}}{{Rg}} = \frac{{N\sin \theta + f\cos \theta }}{{N\cos \theta - f\sin \theta }}
\end{array}\)
\(\begin{array}{l}
For\,vertical\,equilibrium\,on\,the\,road,\\
N\cos \theta = mg + f\sin \theta \\
mg = N\cos \theta - f\sin \theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
Centripetal\,force\,for\,safe\,turning\,,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,N\sin \theta + f\cos \theta = \frac{{m{v^2}}}{R}\,\,\,\,\,\,...\left( {ii} \right)\\
From\,eqns.\,\left( i \right)\,and\,\left( {ii} \right),\,we\,get\\
\,\,\,\,\,\,\,\,\,\,\,\frac{{{v^2}}}{{Rg}} = \frac{{N\sin \theta + f\cos \theta }}{{N\cos \theta - f\sin \theta }}
\end{array}\)
\(\begin{array}{l}
\Rightarrow \,\frac{{{v^2}_{\max }}}{{Rg}} = \frac{{N\sin \theta + {\mu _s}N\cos \theta }}{{N\cos \theta - {\mu _s}N\sin \theta }}\\
\,\,\,\,\,\,{v_{\max }} = \sqrt {Rg\left( {\frac{{{\mu _s} + \tan \theta }}{{1 - {\mu _s}\tan \theta }}} \right)}
\end{array}\)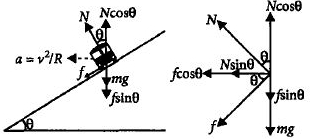
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક રોકેટ ને $2\,g$ પ્રવેગ થી પૃથ્વીથી શિરોલંબ છોડવામાં આવે છે. જ્યાં $g$ એ ગુરુત્વપ્રવેગ છે. રોકેટની અંદર સમક્ષિતિજ થી $\theta $ નો ખૂણો બનાવીને એક ઢોળાવવાળા સમતલ પર $m$ દળ નો પદાર્થ મૂકેલો છે. પદાર્થ ગતિમાન ન થાય તે માટે પદાર્થ અને સમતલ વચ્ચે નો ન્યુનત્તમ ઘર્ષણાંક કેટલો થાય?View Solution
- 2એક કારના તળિયા પર રહેલો પદાર્થ સ્થિર રહે છે. પદાર્થ અને તળિયા વચ્યેનો સ્થિત ઘર્ષણાંક $0.15$ છે.કારનો મહત્તમ પ્રવેગ ($m s ^{-2}$ માં) ગણો.$\left( g =10\,m s ^{-2}\right)$.View Solution
- 3બરફના બ્લોકને $\theta=45^°$ ઢાળવાળા રફ ઢાળ પરથી નીચે આવતા લાગતો સમય એ સમાન ઘર્ષણરહિત ઢાળ પરથી નીચે આવતા લાગતા સમય કરતાં બમણો હોય તો બ્લોક અને ઢાળ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
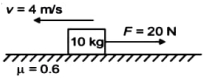
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણો $10 \,kg$ દળનો એક બ્લોક એેક ખરબચડી સપાટી પર ગતિ કરી રહ્યો છે. તો બ્લોક પર લાગતું ઘર્ષણા બળ .... $N$ છે.View Solution
- 5$60\, kg$ નો માણસ થાંભલા પર $600 \,N$ બળ લગાવીને નીચે ઉતરે છે.હાથ અને થાંભલા વચ્ચેનો ઘર્ષણાંક $0.5$ હોય,તો માણસ ........ $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે. $(g = 10\,\,m/{s^2})$View Solution
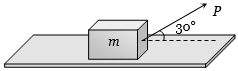
- 6બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $\mu$ હોય તો બ્લોક અને સપાટી વચ્ચે કેટલું ઘર્ષણ બળ લાગતું હશે?View Solution
- 7View Solutionમહતમ સ્થિત ઘર્ષણનુ બીજું નામ શું છે?
- 8View Solutionનીચે આપેલ વિઘાનોમાંથી કયું એક વિધાન અસત્ય છે?
- 9View Solutionસાયું નિવેદન પસંદ કરો.
- 10$m$ દળની એક રેસિંગ કાર $R$ ત્રિજ્યાના સમક્ષિતિજ વર્તુળાકાર માર્ગ (track) પર $v$ વેગથી ગતિ કરે છે. જો ટાયર અને રસ્તા વચ્ચેનો સ્થિત ઘર્ષણાંક $\mu_{s}$ હોય તો કાર પર નીચે તરફ લાગતાં લિફ્ટ બળ $F_{L}$ નું ઋણ મૂલ્ય કેટલું હશે?View Solution
(બધાજ ટાયર દ્વારા લાગતું બળ સમાન ધારો)