\(\overrightarrow{\mathrm{P}}=\cos (\mathrm{kt}) \hat{\mathrm{i}}-\sin (\mathrm{kt}) \hat{\mathrm{j}} ;|\overrightarrow{\mathrm{P}}|=1\)
\(\because \overrightarrow{\mathrm{P}}=\mathrm{m} \overrightarrow{\mathrm{v}}\)
\(\therefore \hat{\mathrm{P}}=\hat{\mathrm{v}}\)
\(\Rightarrow \hat{\mathrm{v}}=\cos (\mathrm{kt}) \hat{\mathrm{i}}-\sin (\mathrm{kt}) \hat{\mathrm{j}}\)
\(\hat{\mathrm{a}}=\frac{-\mathrm{k} \sin (\mathrm{kt}) \hat{\mathrm{i}}-\mathrm{k} \cos (\mathrm{kt}) \hat{\mathrm{j}}}{\mathrm{k}}\)
\(\Rightarrow \hat{\mathrm{a}}=-\sin k t \hat{\mathrm{i}}-\cos k \hat{\mathrm{t}}\)
\(\because \hat{\mathrm{F}}=\hat{\mathrm{a}}=-\sin \mathrm{kt} \hat{\mathrm{i}}-\cos k t \hat{\mathrm{j}}\)
\(\cos \theta=\frac{\hat{\mathrm{F}} \cdot \hat{\mathrm{P}}}{|\hat{\mathrm{F}}| \hat{\mathrm{P}} \mid}=-\frac{\sin k t \cos \mathrm{t}+\sin k t \cos \mathrm{t}}{1 \times 1}=0\)
\(\Rightarrow \theta=\frac{\pi}{2}\)
Download our appand get started for free
Similar Questions
- 1$0.15\, \mathrm{~kg}$ દળ ધરાવતા એક બોલને $10\, m$ ઊંચાઈએથી છોડવામાં આવે છે, તો તે ભોંયતળિયાને અથડાઈને સમાન ઊંચાઇ સુધી રિબાઉન્ડ થાય છે. બોલને અપાતા આવેગનું મૂલ્ય $......$ ની નજીક હશે. $\left(\mathrm{g}=10 \,\mathrm{~m} / \mathrm{s}^{2}\right)$ ($\mathrm{kg}\, \mathrm{m} / \mathrm{s}$ માં)View Solution
- 2શિરોલંબ ઉડાન માટે $5000 \;kg$ નું રોકેટ તૈયાર કરેલ છે. બહાર નીકળતા વાયુની ઝડપ $800\; m/s$ છે. તેને શરૂઆતનો ઉર્ધ્વ પ્રવેગ $20 \;m/s^2$ આપવા માટે, જરૂરી બળ પૂરું પાડવા પ્રતિ સેકન્ડે કેટલો વાયુ ($kg\,s^{-1}$ માં) બહાર કાઢવો જોઈએ?View Solution
($g = 10\;m/s ^2$)
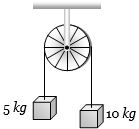
- 3View Solutionઆકૃતિમાં દર્શાવ્યા મુજબ બે દળ ધરાવતા પદાર્થોને હલકી પુલી પરથી લટકાવેલ છે. જયારે પદાર્થને મુકત કરવામાં આવે ત્યારે તંત્રનો પ્રવેગ કેટલો થશે?
- 4સ્થિર રહેલા પદાર્થના એકાએક ત્રણ ટુકડા થાય છે. બે ટુકડાઓનું વેગમાન અનુક્રમે $2\,\,p\,\,\hat i$ અને $\,\,p\,\,\hat j$ છે. જ્યાં, $p$ એ ઘન સંખ્યા છે. ત્રીજા ટુકડાનું ......View Solution
- 5કણનો સ્થાન સદિશ સમય $t$ સાથે $\vec{r}=\left(10 t \hat{i}+15 t^2 \hat{j}+7 \hat{k}\right) \;m$ મુજબ દર્શાવવામાં આવે છે. તો કણે અનુભવેલ પરિણામી બળની દિશા ....... છે.View Solution
- 6$M$ દળના બ્લોકને $M / 2$ દળના દોરડા વડ સક્ષિતિજ ઘર્ષણરહિત સપાટી પર ખેંચવામાં આવે છે. જો દોરડાના એક છેડા પર $2\,mg$ બળ લાગે તો, બ્લોક પર લાગતુ બળ $..........$View Solution
- 7અચળ બળ $\overrightarrow F = {F_x}\hat i + {F_y}\hat j$ હેઠળ એક $5\, kg$ દળનો પદાર્થ $t\,= 0\, s$ સમયે $\overrightarrow v = \left( {6\hat i - 2\hat j\,m/s} \right)$ જેટલો અને $t\, = 10\,s$ સમયે $\overrightarrow v = +6\hat j\,m/s$ જેટલો વેગ ધરાવે છે. તો બળ $\overrightarrow F $ કેટલું થશે?View Solution
- 8$1000\, kg$ દળ ધરાવતી લિફ્ટ ઊર્ધ્વદિશામાં $1\; m/s^2$ ના પ્રવેગથી ગતિ કરે છે. લિફ્ટ સાથે જોડાયેલા દોરડામાં કેટલું તણાવ ($N$ માં) ઉત્પન્ન થશે? $(g= 9.8\ m/{s^2})$View Solution
- 9એક કણ $\overrightarrow{\mathrm{F}}$ બળની અસર હેઠળ $x-y$ સમતલમાં એવી રીતે ગતિ કરે છે કે તેનું રેખીય વેગમાન $\overrightarrow{\mathrm{p}}(\mathrm{t})=\hat{i} \cos (\mathrm{kt})-\hat{j} \sin (\mathrm{kt})$ થી આપી શાકા છે. જો $\mathrm{k}$ એ અચળાંક હોય તો $\overrightarrow{\mathrm{F}}$ અને $\overrightarrow{\mathrm{p}}$ વચ્ચેનો કોણ. . . . . . . .થશે.View Solution
- 10$20 \,kg$ નો વાંદરો ઊભી દોરડું પકડે છે. જો દોરડા પર $25\,kg$ નું દળ લટકાવવામાં આવે, તો દોરડું તૂટતું નથી, પરંતુ જો તેના પર $25\,kg$ થી વધુ દળ લટકાવવામાં આવે તો તે તૂટી જશે. તે મહત્તમ કેટલા પ્રવેગથી ($m/{s^2}$ માં) વાંદરો દોરડા પર ચઢી શકે? $(g = 10\,m/{s^2})$View Solution
