(b)
Retardation \(\rightarrow a\)
Initial velocity \(\rightarrow u\)
\((I)\) For total journey
\(v=u+a t\)
\(0=u-a T\)
\(\Rightarrow u=a T \ldots (i)\)
\(d=u T-\frac{1}{2} a T^2\)
Dividing by \(2\) on both sides
\(\frac{d}{2}=\frac{u T}{2}-\frac{1}{2} \frac{a T^2}{2} \ldots (ii)\)
On comparing equation \((i)\) and \((iii)\)
\(\frac{u T}{2}-\frac{1}{2} \frac{a T^2}{2}=u t-\frac{1}{2} a t^2\)
Put \(u=a T\)
\(\Rightarrow \frac{a T^2}{2}-\frac{a T^2}{4}=a T t-\frac{1}{2} a t^2\)
\(\Rightarrow \frac{T^2}{4}=T t-\frac{t^2}{2}\)
Multiplying by 4 on both sides
\(T^2=4 T t-2 t^2 \Rightarrow 2 t^2-4 T t+T^2=0\)
On solving this quadratic equation,
\(t=T-\frac{T}{\sqrt{2}} \Rightarrow t=T\left(1-\frac{1}{\sqrt{2}}\right)\)
\((II)\) For half journey
\(\frac{d}{2}=u t-\frac{1}{2} a t^2 \ldots (iii)\)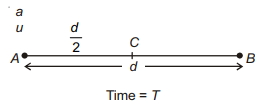
Download our appand get started for free
Similar Questions
- 1ટ્રેન $A$ અને ટ્રેન $B$ સમાંતર ટ્રેક પર વિરુદ્ધ દિશામાં અનુક્રમે $36\, km / hour$ અને $72 \,km / hour$ ની ઝડપથી ગતિ કરે છે. ટ્રેન $A$ પર એક વ્યક્તિ ગતિની વિરુદ્ધ દિશામાં $1.8\, km / hr$ ની ઝડપથી ગતિ કરે છે. ટ્રેન $B$ પરથી અવલોકન કરતાં વ્યક્તિને તે કેટલી ઝડપથી ($ms ^{-1}$) ગતિ કરતો જણાશે?View Solution
(બંને ટ્રેક વચ્ચેનું અંતર નહિવત લો)
- 2સ્થિર સ્થિતિમાંથી અચળ પ્રવેગી ગતિ કરતો કણ પ્રથમ $2 \;sec$ માં કાપેલ અંતર $x $ અને તેની પછીની $2\; sec$ માં કાપેલ અંતર $y$ છે,તો તેમની વચ્ચેનો સંબંધ શું થાય?View Solution
- 3બે કણ $A$ અને $B$ માટે સ્થાનાંતર વિરુદ્ધ સમયનો ગ્રાફ સુરેખ મળે છે જેનો સમયની અક્ષ સાથેનો ખૂણો ${30^o}$ અને ${60^o}$ છે તો તેમના વેગનો ગુણોત્તર ${V_A}:{V_B}$ કેટલો થાય?View Solution
- 4એક કાર $X$ સ્થાનથી $Y$ સ્થાન સુધી અચળ ઝડપ $v_1$ અને પાછી $X$ સ્થાને અચળ ઝડપ $v_2$ થી આવે છે. તેની આ મુસાફરી દરમિયાનની સરેરાશ ઝડપ કેટલી થાય?View Solution
- 5View Solutionનીચેનાં બધાં જ આલેખો એક સમાન ગતિને રજૂ કરે છે. તેમાંનો કોઇ એક તેને ખોટી રીતે રજૂ કરે છે. તે શોધો.
- 6સમય અને અંતર વચ્ચેનો સંબંધ $t = \alpha {x^2} + \beta x$ છે, જ્યાં $\alpha $ અને $\beta $ અચળાંકો છે. પ્રતિપ્રવેગ કેટલો થાય?View Solution
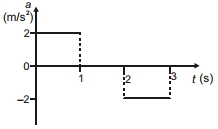
- 7કણ માટે પ્રવેગ સમયનો આલેખ આકૃતિમાં આપવામાં આવ્યો છે. જો તે $t=0$ પર ગતિ શર કરે છે, તો $3$ સેક્ન્ડમાં કાણ દ્વારા કપાયેલ અંતર .......... $m$ હશે?View Solution
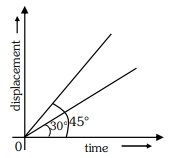
- 8$x$-અક્ષ સાથે $30^{\circ}$ અને $45^{\circ}$ નો કોણ સાથે ગતિ કરતા બે કણો માટે સ્થાનાંતર-સમયના આલેખો આકૃતિમાં દર્શાવ્યા છે. તેઓનો અનુક્રમે વેગોનો ગુણોતર ....... હશે.View Solution
- 9જો $t =\sqrt{ x }+4$ છે, તો $\left(\frac{ dx }{ dt }\right)_{ t =4}$ નું મૂલ્ય.View Solution
- 10એક પદાર્થ $x=0$ સ્થાને સ્થિર સ્થિતિમાં છે. તે $t=0$ સમયે ધન $x$ દિશામાં અચળ પ્રવેગી ગતિ શરૂ કરે છે. આ જ સમયે બીજો એક પદાર્થ પણ $x =0$ સ્થાનેથી ધન $x$ દિશામાં અચળ ઝડપથી ગતિ કરે છે. $t$ સમય પછી પ્રથમ પદાર્થનું સ્થાન $x _{1}(t)$ વડે તથા સમાન સમય અંતરાલ પછી બીજા પદાર્થનું સ્થાન $x _{2}(t)$ વડે અપાય છે. નીચેનામાંથી ક્યો આલેખ $\left( x _{1}- x _{2}\right)$ ને સમય $t$ ના વિધેય તરીકે સાચી રીતે દર્શાવે છે?View Solution
