એક કણ તેના ઉગમ બિંદુથી $xy$ સમતલમાં વર્તુળાકાર માર્ગ પર ગતિ કરે છે. જો કોઈ સમયે કણની સ્થાનને $\frac{1}{\sqrt{2}}(\hat{i}+\hat{j})$, દ્વારા દર્શાવી શકાય તો કણનો વેગ શું હશે?
Diffcult
d
(d)
(d)
\(\vec{r}=\frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}} \hat{j}\)
\(\vec{v} \cdot \vec{r}=0\) as velocity is always tangential to the path.
\(\left(v_x \hat{i}+v_y \hat{j}\right) \cdot \frac{1}{2}(\hat{i}+\hat{j})=0\)
\(v_x+v_y=0\)
\(\Rightarrow v_x=-v_y\)
\(\text { or }\)
\(v_y=-v_x\)
\(v=\sqrt{v_x^2+v_y^2} \quad \Rightarrow \sqrt{2} v_x=v \Rightarrow v_x=\frac{v}{\sqrt{2}}\)
\(v_y=-\frac{v}{\sqrt{2}}\)
\(\text { or } v_x=-\frac{v}{\sqrt{2}}, v_y=\frac{v}{\sqrt{2}}\)
So, possible value of \(v \Rightarrow v_x \hat{i}+v_y \hat{j} \Rightarrow \frac{v}{\sqrt{2}} \hat{i}-\frac{v}{\sqrt{2}} \hat{j}\) or \(\frac{-v}{\sqrt{2}} \hat{i}+\frac{v}{\sqrt{2}} \hat{j}\)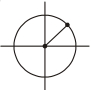
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લડાકુ વિમાન અમુક ઊંચાઈએ સમકક્ષિતિજ રીતે $200 \,ms ^{-1}$ ની ઝડપપી ઉડી રહ્યું છે. તે anti-aircraft gun ની બરાબર ઉપરથી પસાર થાય છે. જો આ ગન દ્વારા લડાકુ વિમાનને ગોળી મારવી હોય તો, સમક્ષિતિજથી,........... ડીંગ્રી એ ગોળી છોડવી પડશે. બુલેટ (ગોળી) ની ઝડ૫ $400 \,m / s$ છે.View Solution
- 2એક બોટ નદીના બે સ્થળો વચ્ચેના અમુક અંતરને આવરી લે છે, જે નદી નીચે તરફ જવા $t$ સમય લે છે અને ઉપરની તરફ જવા $t_2$ સમય લે છે. બોટ દ્વારા સ્થિર પાણીમાં એ જ અંતરને આવરવા માટે કેટલો સમય લાગશે?View Solution
- 3બંદૂકમાંથી એક ગોળી $280\,m s ^{-1}$ ની ઝડપે સમક્ષિતિજની ઉપર $30^{\circ}$ ને ખૂણે છોડવામાં આવે છે. ગોળીએ પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $.......\,m$ છે.$\left( g =9.8\,m s ^{-2}, \sin 30^{\circ}=0.5\right)$View Solution
- 4એક પદાર્થને $25 \,m/s$ ના વેગથી પ્રક્ષિપ્ત કરતા તે $2\, sec$ પછી $ 5\,m$ ઊંચાઇ ધરાવતી દિવાલને પસાર કરે છે,તો પ્રક્ષિપ્ત કોણ ...... $^o$ હશે. $(g = 10m/{\sec ^2})$View Solution
- 5સમક્ષિતિજ સાથે $40^{\circ}$ અને $50^{\circ}$ ના ખૂણે અનુકમે બે પ્રક્ષેપણ $A$ અને $B$ કરવામાં આવે છે. જેમનો વેગ સમાન છે.પછી $.............$View Solution
- 6એક લડાકુ વિમાન અમુક ઊંચાઈએ સમકક્ષિતિજ રીતે $200 \,ms ^{-1}$ ની ઝડપપી ઉડી રહ્યું છે. તે anti-aircraft gun ની બરાબર ઉપરથી પસાર થાય છે. જો આ ગન દ્વારા લડાકુ વિમાનને ગોળી મારવી હોય તો, સમક્ષિતિજથી,........... ડીંગ્રી એ ગોળી છોડવી પડશે. બુલેટ (ગોળી) ની ઝડ૫ $400 \,m / s$ છે.View Solution
- 7ચોક્કસ ગ્રહ (કોઈ વાતાવરણ વિના) પર જમીન પરથી ઉદ્ભવેલ પ્રક્ષેપણની સ્થાનનું નિર્દેશન $y=\left(4 t-2 t^2\right) m$ અને $x=(3 t) m$ દ્વારા આપવામાં આવે છે, જ્યાં $t$ સેકન્ડમાં છે અને પ્રક્ષેપણના બિંદુને ઉગમબિંદુ તરીકે લેવામાં આવે છે. શિરોલંબ સાથે પ્રક્ષિપ પદાર્થનો પ્રક્ષેપણ ખૂણો કેટલો હોય?View Solution
- 8પ્રાક્ષિપ્ત પદાર્થનું સમીકરણ $y=a x-b x^2$ છે. તેની સમક્ષિતીજ અવધી શું હશે?View Solution
- 9ચોક્કસ સમયે વર્તુળાકાર ગતિ કરતા કણના વેગના અને પ્રવેગ સદિશો અનુક્રમે $\vec{v}=2 \hat{i} m / s$ અને $\vec{a}=2 \hat{i}+4 \hat{j} m / s^2$ છે.તો વર્તુળની ત્રિજ્યા $ ........\,m$View Solution
- 10View Solutionઅચળ મુલ્યનું બળ બે કણની ગતિની દિશાને લંબ લાગે છે, તો પછી તેની
