એક ક્ષ કિરણ $50\, kV$ પર કાર્ય કરે છે. જે $1\%$ ઊર્જાને ક્ષ કિરણના સ્વરૂપમાં રૂપાંતરિત કરે છે. જો ઉત્પન્ન થતી ઉષ્માનો જથ્થો $495$ વોટ હોય તો ટાર્ગેંટ સાથે પ્રતિ સેકન્ડે અથડાતા ઈલેક્ટ્રોનની સંખ્યા .....છે.
Medium
Download our app for free and get started
a
\(\frac{{{\text{Heat}}}}{{{\text{Time}}}} = \left( {1 - \frac{\eta }{{100}}} \right)\,VI\,\,\)
\(\frac{{{\text{Heat}}}}{{{\text{Time}}}} = \left( {1 - \frac{\eta }{{100}}} \right)\,VI\,\,\)
\(\,\,\, \Rightarrow \,\,\,495 = \left( {1 - \frac{1}{{100}}} \right)\,\,50 \times {10^3}(I)\)
\( \Rightarrow \,I = \frac{{495 \times 100}}{{99 \times 50 \times {{10}^3}}} = 10\,\,mA\,\,\,\,\)
\(\therefore\) \(\frac{N}{t} = \frac{I}{e} = \frac{{10 \times {{10}^{ - 3}}}}{{1.6 \times {{10}^{19}}}} = 6.25 \times {10^{16}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હાઇડ્રોજન પરમાણુમાં ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનની ઊર્જા $ -13.6\; eV $ છે, જ્યારે ઇલેક્ટ્રોન પ્રથમ ઉત્તેજિત અવસ્થામા હોય, ત્યારે ઇલેકટ્રોનની ઉત્તેજિત ઊર્જા ($eV$ માં) કેટલી હશે?View Solution
- 2View Solutionજો ક્ષ કિરણો તીવ્ર ચુંબકીય ક્ષેત્રમાંથી પસાર થાય તો ક્ષ કિરણો. . . . . .
- 3${\lambda _x}$ અને ${\lambda _y}$ તરંગલંબાઈ ધરાવતા બે કણના સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણથી કણ $P$ બને છે.જો $x$ અને $y$ વિરુદ્ધ દિશામાં ગતિ કરતાં હોય તો કણ $P$ ની દ-બ્રોગ્લી તરંગલંબાઈ કેટલી થાય?View Solution
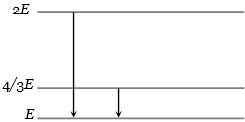
- 4$2E$ ઊર્જા ધરાવતી કક્ષામાંથી $E$ ઊર્જા ધરાવતી કક્ષામાં સંક્રાતિ દરમિયાન $ \lambda $ તરંગલંબાઇનું ઉત્સર્જન થાય છે,તો $ \frac{{4E}}{3} $ ઊર્જા ધરાવતી કક્ષામાંથી $E$ ઊર્જા ધરાવતી કક્ષામાં સંક્રાતિ દરમિયાન કેટલી તરંગલંબાઇનું ઉત્સર્જન થાય?View Solution
- 5હાડકમાં ફ્રેકચર શોધવામાં લઘુતમ તરંગલંબાઈ $10^{11}\,m$ હોય તો $x-ray$ મશીન માં વૉલ્ટેજ.View Solution
- 6બોહરના પરમાણુ મોડલમાં ઇલેક્ટ્રોન $0.5 \times 10^{-10}\,m$ ત્રિજયાની વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે તેવું ધારવામાં આવ્યું છે. જો ઇલેક્ટ્રોનની ઝડપ $2.2 \times 10^{6}\; {m} / {s}$હોય, તો ઇલેક્ટ્રોન સાથે સંકળાયેલ પ્રવાહ $....\,\times 10^{-2} \;{mA}$ હશે. $\left.[\pi=\frac{22}{7}\right]$View Solution
- 7હાઈડ્રોજનનો પરમાણુ ધરાસ્થિતિમાંથી ઉત્તેજિત થઈને મુખ્ય ક્વૉન્ટમ નંબર $4$ ધરાવતી અવસ્થામાં જાય છે. તો મળતાં ઉત્સર્જન વર્ણપટમાં કેટલી વર્ણપટ રેખાઓ મળશે ?View Solution
- 8View Solutionચોક્કસ પરમાણુમાં ઈલેક્ટ્રોન માટે ઊર્જા સ્તરો આકૃતિમાં દર્શાવ્યો છે. નીચેના પૈકી કઈ સંક્રાતિ, સૌથી વધુ ઊર્જા સાથે ફોટોનનું ઉત્સર્જન કરશે?
- 9હાઈડ્રોજન પરમાણુ $975\, Å$ તરંગ લંબાઈના વિકિરણ ભૂમિ અવસ્થામાંથી ઉત્તેજીત અવસ્થામાં આવે છે. ઉત્સર્જન વર્ણપટમાં કેટલી રેખાઓ શક્ય છે?View Solution
- 10ધરાસ્થિતિએ રહેલો હાઈડ્રોજન પરમાણુ $5$ નાં મુખ્ય ક્વોન્ટમ અંકની સ્થિતિ સુધી ઉત્તેજીત થાય છે. તો વર્ણપટમાં કેટલી રેખાઓ જોવાં મળશે?View Solution