એક ક્ષેત્રમાં એકસમાન વિદ્યુતક્ષેત્ર પ્રવર્તે છે. આ ક્ષેત્રમાં બિંદુ $P$ આગળ કેન્દ્ર હોય તેવા ગોળા પરના અલગ અલગ બિંદુ આગળનું વિદ્યુતસ્થિતિમાન $589.0\,V$ થી $589.8\, V$ જેટલું બદલાય છે. વિદ્યુતક્ષેત્ર સાથે $60^o$ નો ખુણો બનાવતા સ્થાન સદીશ પર રહેલ ગોળા પરના બિંદુ આગળ વિદ્યુતસ્થિતિમાન ($V$ માં) કેટલું હશે?
JEE MAIN 2017, Diffcult
Download our app for free and get started
c
Potential gradient is given by,
Potential gradient is given by,
\(\Delta \mathrm{V}=\mathrm{E} . \mathrm{d}\)
\(0.8=\mathrm{Ed}(\mathrm{max})\)
\(\Delta V=E d \cos \theta=0.8 \times \cos 60=0.4\)
Hence, maximum potential at a point on the sphere
\(=589.4\, \mathrm{V}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$a$ અને $b$ ત્રિજયાની ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે.બંને કવચ વચ્ચેનું માધ્યમ હવા છે.બહારની ગોળીય કવચ અને અંદરની ગોળીય કવચ વારાફરતી ગ્રાઉન્ડ કરવાથી બનતા કેપેસિટન્સ નો તફાવત કેટલો થાય? $(b>a)$View Solution
- 2$2 \times 10^{-2}\,C$ નો એક બિંદુવત વિદ્યુતભાર $P$ થી $S$ સુધી ધન $x-$ અક્ષની દિશામાં પ્રવર્તતા $30\,NC ^{-1}$ જેટલા નિયમિત વિદ્યુતક્ષેત્રમાં ગતિ કરે છે. જો $P$ અને $S$ના યામો અનુક્રમે $(1,2,0),(2,0,0),(1,-2,0)$ અને $(0,0,0)$ હોય, તો આ પ્રક્રિયામાં થતું કાર્ય $.........\,mJ$ થશે.View Solution
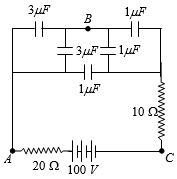
- 3આપેલ તંત્ર માં બિંદુ $A$ અને $B$ વચ્ચેનો વિદ્યુતસ્થિતિમાન અને બિંદુ $B$ અને $C$ વચ્ચેનો વિદ્યુતસ્થિતિમાન કેટલો થાય?View Solution
- 4View Solutionવિદ્યુતભારિત વાહક ગોળા માટે કયું વિધાન સાચું નથી?
- 5$q$ વિદ્યુતભારને સ્થિર $Q$ વિદ્યુતભાર તરફ $v$ ઝડપથી ફેકવામાં આવે છે. તે $Q$ ની નજીક $r$ અંતર સુધી જઇ શકે છે અને પછી પરત આવે છે. જો $q$ વિદ્યુતભારને $2v$ ઝડપ આપવામાં આવે તો તે કેટલો નજીક જશે?View Solution
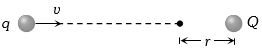
- 6View Solutionપુરો વિદ્યુતભાર થયેલા એક સમાંતર પ્લેટવાળા કેેેસીટરને બેટરી સાથે જોડેલ રાખીને અવાહક સાધનો વડે તેની પ્લેટોને એકબીજાથી દૂર કરવામાં આવે છે. આ સ્થિતિમાં નીચેનામાંથી કઈ રાશિનું મૂલ્ય ઘટશે?
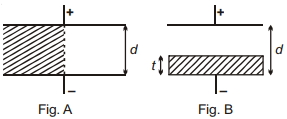
- 7આકૃતિમાં $A$ દર્શાવ્યા મુજબ એક કેપેસીટર ડાઈઈલેક્ટ્રીક ($K=2$) વડે અડધો ભરાયેલ છે. જો આકૃતિનાં બીજા ભાગ $B$ પ્રમાણે તે અડધો ભરાયેલ હોય તો ડાઈઈલેક્ટ્રીકની એવી જાડાઈ શોધો કે જેનાથી કેપેસીટરની ક્ષમતા એટલી જ રહે?View Solution
- 8$20\, C$ નો એક વિદ્યુતભાર $2 \,cm$ અંતરે ગતિ કરે છે. થતું કાર્ય $2 \,J$ છે. તો બે બિંદુઓ વચ્ચેનો સ્થિતિમાનનો તફાવત ........$V$ છે.View Solution
- 9$1\, g$ દળ તથા $10^{-8}\ C$ વિદ્યુતભાર ધરાવતો બોલ $600\, volt$ વિદ્યુત સ્થીતીમાન ધરાવતા બિંદુ $A$ થી શુન્ય $(0) \,volt$ વિદ્યુતસ્થીતીમાન ધરાવતા બિંદુ $B$ પર જાય છે. બિંદુ $B$ આગળ બોલનો વેગ $20\,cm/s$ છે તો બિંદુ $A$ આગળ બોલનો વેગ......$cm/s$View Solution
- 10એક વિદ્યુત પરિપથમાં $1.0$ $kV$ વિદ્યુત વિભવની સામે $2$$\mu F$ કેપેસિટરોની જરૂર છે.$1$$\mu F$ ના ખૂબ જ મોટી સંખ્યામાં કેપેસિટરો છે,જે $300$ $V$ ના વિદ્યુત વિભવ કરતા વધુ વિદ્યૂત વિભવ સહિ શકતા નથી. તો આ માટે જરૂરી ઓછામાં ઓછા કેપેસિટરોની સંખ્યાView Solution