પ્રારંભમાં તંત્ર સ્થિર છે તેમ આપેલ છે એટલે કે \(\,{\overrightarrow {\text{v}} _{CM}}\,\, = \,\,0\) હવે, આંતરિક બાળ એ ઉપર ચઢવા માટેનું બળ છે.
તેથી, \({\overrightarrow {\text{v}} _{CM}}\,\, = \,\,0\) અચલ \(\, = \,\,0\) એટલે કે \(\frac{{m\overrightarrow v \,\, + \;\,M\overrightarrow V }}{{m\,\, + \;\,M}}\,\, = \,\,0\) અથવા \(m\overrightarrow v \,\, + \;\,M\overrightarrow V \,\, = \,\,0\,\,\,\,......\left( i \right)\,\)
અથવા \(m\,\frac{{\Delta {{\overrightarrow r }_1}}}{{\Delta t}}\,\, + \;\,M\,\,\frac{{\Delta {{\overrightarrow r }_2}}}{{\Delta t}}\,\, = \,\,0\)
\(m\Delta \,{\overrightarrow r _1}\,\, + \;\,M\,\Delta {\overrightarrow r _2}\, = \,\,0\,\,\,\,\left[ {\,\,\because \,\,\,\Delta \overrightarrow r \,\, = \,\,\overrightarrow d \,\,} \right]\)
\(m{\overrightarrow d _1}\,\, + \;\,M{\overrightarrow d _2}\,\, = \,\,0\,\,\) અથવા \(m{d_1}\,\, - \,\,M{d_2}\,\, = \,\,0\) [ \({\because \,\,{{\overrightarrow d }_2}}\) એ \({{{\overrightarrow d }_1}}\) થી વિરુદ્ધ છે . ] અથવા \(m{d_1}\,\, = \,\,M{d_2}\,\,\,\,....\left( {ii} \right)\)
હવે,વાંદરો બ્લૂનની દિશામાં \(L\) સુધી ચઢે છે (બ્લૂનની સાપક્ષે),બલૂન \(2 \) જેટલું જમીનની સાપેક્ષે નીચે ઉતરે છે.
તેથી, જમીનની સાપેક્ષે માણસનું ઉર્ધ્વ સ્થાનાંતર, \(1 = L - d_2 …..(iii) (i.e. d_1 + d_2 = L)\)
સમીકરણ \((ii) \) અને \((iii)\) પરથી , \(m(L - d_2) = Md_2\)
\({d_2}\,\, = \,\,\frac{{mL}}{{m\,\, + \;\,M}}\)
Download our appand get started for free
Similar Questions
- 1પદાર્થ પર $50 \,N$ બળ લાગતાં તે બળની દિશા સાથે $60^°$ ના ખૂણે $10\, meter$ સ્થાનાંતર કરે,તો કાર્ય ......... $J$ મેળવે.View Solution
- 2પદાર્થ પર $ F = (5\hat i + 3\hat j) $ બળ લાગતાં તેનું સ્થાનાંતર $ r = (2\hat i - 1\hat j) $ થાય,તો કાર્ય કેટલા .....$joules$ થાય?View Solution
- 3$m$ દળ અને $2\, v$ વેગ ધરાવતો પદાર્થ તે જ દિશામાં જતાં $2\,m$ દળ અને $v$ વેગથી ગતિ કરતા પદાર્થ સાથે અથડાય છે. અથડામણ પછી પ્રથમ પદાર્થ ઊભો રહી જાય છે છે જ્યાંરે બીજો પદાર્થ બે $m$ દળના પદાર્થમાં વિભાજિત થાય છે.જે શરૂઆતની દિશા સાથે $45^o$ ના ખૂણે ગતિ કરે તો ગતિ કરતાં દરેક પદાર્થનો વેગ કેટલો હશે?View Solution
- 4$2kg $ નો પદાર્થ $3 m/sec$ ના વેગથી વિરુધ્ધ દિશામાં આવતા $ 4 m/s$ ના $1 kg $ ના પદાર્થ સાથે અથડાતા બંને પદાર્થ ચોંટી જાય છે.તો તેમનો સંયુકત વેગ કેટલો થાય?View Solution
- 5$M$ દળવાળા બ્લોકને સ્પ્રિંગના નીચેના છેડે લગાડવામાં આવે છે. સ્પ્રિંગને છત સાથે લટકાવેલ છે અને તેનો બળ અચળાંક $k$ છે. બ્લોકને સ્પ્રિંગની ખેંચાણ વગરની મૂળ સ્થિતિમાંથી મુકત કરવામાં આવે છે. સ્પ્રિંગની લંબાઇમાં થતો મહત્તમ વધારો કેટલો હશે?View Solution
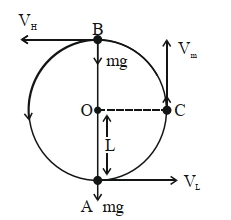
- 6$'m'$દળ ધરાવતા દોલકને $'L'$ લંબાઇની હલકી દોરી વડે લટકાવવામાં આવે છે. તેના સૌથી નીચિના બિંદુ $A$ આગળ એવી રીતે લધુત્તમ સમક્ષિતિજ વેગ લગાડવામાં આવે છે કે જેથી તે અર્ધ વર્તુળાકાર ગતિ કરી સૌથી ઉપરના સ્થાન આગળ પહોંચે છે. તેમની ગતિ ઊર્જાઓની ગુણોત્તર $\frac{(K . E)_A}{(K . E)_B}$________છે:View Solution
- 7પદાર્થ પર $ \overrightarrow {F\,} = 6\hat i + 2\hat j - 3\hat k $ બળ લાગતાં તેનું સ્થાનાંતર $ \overrightarrow {s\,} = 2\hat i - 3\hat j + x\hat k. $ થાય,જો કાર્ય શૂન્ય હોય,તો $x=$____View Solution
- 8કારને $ F$ અવરોધકબળ લાગતાં $s$ અંતર કાપીને સ્થિર થાય છે.જો કારનું દળ $ 50 \%$ વધે તેા કેટલા.....$s$ અંતરે કાર સ્થિર થશે?View Solution
- 9$2\ kg$ ના એક પદાર્થ પર એક બળ એવી રીતે લગાડવામાં આવે છે કે તેની સ્થિતિને સમય વિધેય $x=3t^2+5$ વડે આપવામાં આવે છે. પ્રથમ $5\ s$ માં આ બળ વડે કેટલા .......... $\mathrm{J}$ કાર્ય થશે?View Solution
- 10$m$ દળ એક બ્લોક ને $\frac{g}{3}$ અચળ પ્રવેગે શિરોલંબ રીતે ઉપર તરફ $h$ અંતર જેટલું ખેંચવા માટે એક દોરીના ઉપયોગ કરવામાં આવે છે. દોરીમાંના તણાવ વડે થયેલ કાર્ય છે...View Solution
