નળાકાર કેપેસિટરનું કેપેસિટન્સ
\(C\,\, = \,\,\frac{{2\pi {\varepsilon _0}\ell }}{{{{\log }_e}\,\left( {\frac{b}{a}} \right)}}\,\, \Rightarrow \,\,Length\,\,\,L\,\, = \,\,\frac{C}{{2\pi { \in _0}}}\,\,{\log _e}\,\,\left( {\frac{b}{a}} \right)\)
અહિં \(C-\) અચળ છે.
\(\therefore \,\,L\,\, = \,\,{\log _e}\,\,\left( {\frac{b}{a}} \right)\)
\(\frac{{{L_1}}}{{{L_2}}}\,\, = \,\,\frac{{{{\log }_e}\,\,\left( {\frac{{{b_1}}}{{{a_1}}}} \right)}}{{{{\log }_e}\,\,\left( {\frac{{{b_2}}}{{{a_2}}}} \right)}}\,\, = \,\,\frac{{{{\log }_e}\left( {10} \right)}}{{{{\log }_e}\,\,\left( {20} \right)}}\)
અહી \(\frac{{{{\text{b}}_{\text{1}}}}}{{{{\text{a}}_{\text{1}}}}}\,\, = \,\,\frac{{10}}{1},\,\,\frac{{{b_2}}}{{{a_2}}}\,\, = \,\,\frac{{20}}{1}\)
\(\therefore \,\,\frac{{{L_2}}}{{L1}}\,\, = \,\,1.3\)
Download our appand get started for free
Similar Questions
- 1$20\, C$ નો એક વિદ્યુતભાર $2 \,cm$ અંતરે ગતિ કરે છે. થતું કાર્ય $2 \,J$ છે. તો બે બિંદુઓ વચ્ચેનો સ્થિતિમાનનો તફાવત ........$V$ છે.View Solution
- 2કોઈ સમાંતર પ્લેટ કેપેસિટરની દરેક પ્લેટનું ક્ષેત્રફળ $1\, m^2$ અને તેમની વચ્ચેનું અંતર $0.1\, m$ છે. જો બે પ્લટો વચ્ચેનું વિદ્યુત ક્ષેત્ર $100 \,N/C$ હોય તો દરેક પ્લેટ પરના વિધુતભારનું મૂલ્ય કેટલું થશે?View Solution
- 3$10\,\mu F$ ની સંઘારકતા ધરાવતા બે સમાંતર પ્લેટ સંઘારકો $C _1$ અને $C _2$ ને સ્વતંત્ર રીતે $100\,V\,D.C.$ ઉદગમથી વિદ્યુતભારિત કરવામાં આવે છે. સંઘારક $C _1$ ને ઉદગમ સાથે જોડેલા રાખીને તેની પ્લેટોની વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. સંઘારક $C _2$ એ ઉદગમથી છુટ્ટો કર્યા પછી તેની પ્લેટો વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. ત્યાર બાદ સંઘારક $C _1$ ને પણ ઉદગમથી છુટું કરી અંતમાં બંને સંઘારકોને સમાંતર જોડાણમાં જોડવામાં આવે છે. આ સંયોજનનું સામાન્ય સ્થિતિમાન $............\,V$ થશે.(ડાયઈલેક્ટ્રીક અચળાંક $=10$ છે તેમ ધારો)View Solution
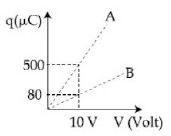
- 4કેપેસીટરના શ્રેણી અને સમાંતર જોડાણ માટે $q$ વિરુદ્ધ $V$ નો આલેખ આપેલ છે.તો આ કેપેસીટરના મૂલ્યો....View Solution
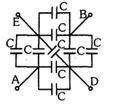
- 5આપેલ આકૃતિમાં $\frac{{{{\text{C}}_{{\text{DE}}}}}}{{{{\text{C}}_{{\text{AB}}}}}}$ ગુણોતર શોધો.View Solution
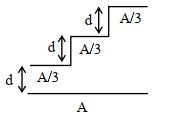
- 6ક્ષેત્રફળ $A$ ધરાવતા સપાટ પ્લેટની મદદથી એક સંધારક રચવામાં આવે છે અને બીજી પ્લેટ આકૃત્તિમાં દર્શાવ્યા અનુસાર સીડી-આકારની રચના ધરાવે છે. જો દરેક સીડીનું ક્ષેત્રફળ $\frac{A}{3}$ અને ઊંચાઈ $d$ હોય તો આ ગોઠવણની સંધારકતા ........... છે.View Solution
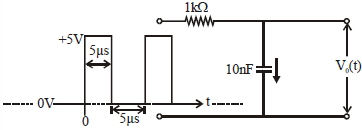
- 7ઈનપુટ વૉલ્ટેજ $V_{\text {in }}( t )$ માટે આઉટપુટ વૉલ્ટેજ કેપેસિટર વ્ચ્ચે $V _{ D }( t ),$ નો આલેખView Solution
- 8View Solutionવિદ્યુત ક્ષેત્રની ઊર્જા ઘનતા કોના સમપ્રમાણમાં હોય છે?
- 9$C$ કેપેસિટન્સ વાળા કેપેસિટરને $V$ સ્થિતિમાને વિદ્યુતભારીત કરવામાં આવે છે. ત્યારે તેને બહાર લઈ અને સમાન વિદ્યુતભાર રહિત કેપેસિટર સાથે સમાંતરમાં જોડવામાં આવે છે. તો દરેક કેપેસિટર પરનો વિદ્યુતભાર શોધો.View Solution
- 10$20\, C$ નો એક વિદ્યુતભાર $2 \,cm$ અંતરે ગતિ કરે છે. થતું કાર્ય $2 \,J$ છે. તો બે બિંદુઓ વચ્ચેનો સ્થિતિમાનનો તફાવત ........$V$ છે.View Solution
