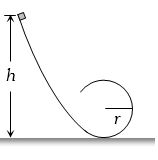
એક પદાર્થ આકૃતિ મુજબ મુકવામાં આવેલ છે.તે પદાર્થને માત્ર એક પરિભમણ પૂરું કરવા માટે $h=$ _____

Medium
d
(d) In order to complete a full circle, the normal force when the block is at the highest point of circular ramp should be greater than zero,
(d) In order to complete a full circle, the normal force when the block is at the highest point of circular ramp should be greater than zero,
\(\mathrm{SO}\)
if value of point \(B=v_{B}\) Then,
At point \(B, m g+N=\frac{m v_{B}^{2}}{R}\)
\(\mathrm{AS} N>0\)
\(\Rightarrow v_{B}^{2}>m g R\)
At point \(-A\)
\(\frac{m v_{A}^{2}}{2}-\frac{m v_{B}^{2}}{2}=m g(2 R)[A s \Delta K E=-\Delta P E]\)
\(\frac{m v_{A}^{2}}{2}=2 m g R+\frac{m v_{B}^{2}}{2}\)
As \(v_{B}^{2}>m g R\)
\(\Rightarrow \frac{m v_{A}^{2}}{2}>2 m g R+\frac{m g R}{2} \Rightarrow \frac{m v_{A}^{2}}{2}>\frac{5 m g R}{2}\)
Also, \(\frac{m v_{A}^{2}}{2}-0=m g h\)
\(\mathrm{As}, m v_{A}^{2}>5 m g R \Rightarrow m g h>\frac{5 m g R}{2}\)
\(\Rightarrow h>5 r/ 2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1\; kg$ દળ ધરાવતો પદાર્થ સમય આધારિત બળ $\vec{F}=\left(\hat{i}+3 t^2 \hat{j}\right) N$ ની અસર હેઠળ ગતિ કરે છે, જ્યાં $\hat{i}$ અને $\hat{j}, x$ અને $y$ અક્ષની દિશામાં એકમ સદિશો છે. આ બળ વડે $t=2 s$ સમયે ઉદભવતો પાવર $...........$ $W$ હશે.View Solution
- 2એક પદાર્થ સ્થિર સ્થિતિમાં રહેલાં બીજા સ્થિર પદાર્થ સાથે સ્થિતિ સ્થાપક રીતે ત્રાંસી દિશામાં અથડાય છે. સંઘાત પછી તેઓ એકબીજાને .............. $^o$ ખૂણે ગતિ કરે.View Solution
- 3View Solutionતંત્રની સ્થિતિઊર્જા વધે જો થતું કાર્ય ....
- 4$4\,g$ અને $16\, g$ ધરાવતાં બે દળોની ગતિ ઊર્જા એક સરખી છે. જે તેમનાં રેખીય વેગમાનનો માનાંકનો ગુણોત્તર $n : 2$ છે. $n$ નું મૂલ્ય ....... હશે.View Solution
- 5$A $ અને $ B$ એમ બે કણો અચળ વેગ અનુક્રમે $\overrightarrow {{v_1}} $ અને $\overrightarrow {{v_2}} $ થી ગતિ કરે છે. પ્રારંભમાં તેના સ્થાન સદિશો અનુક્રમે $\overrightarrow {{r_1}} $ અને $\overrightarrow {{r_2}} $ છે. $A$ અને $B $ ના સંઘાત માટેની શરત શું થાય?View Solution
- 6જો $F=2 x^2-3 x-2$, તો સાયું વિધાન પસંદ કરોView Solution
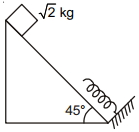
- 7આકૃતિમાં દર્શાવ્યા મુજબ $\sqrt{2} \,kg$ દળ વાળા એક બ્લોકને એક ઢોળાવવાળી લીસી સપાટીની ટોચ પરથી છોડવામાં આવે છે. જો સ્પ્રિંગ નો સ્પ્રિંગ અચળાંક $100 \,N / m$ હોય અને ને $1 \,m$ સંકોચાયા બાદ બ્લોક સ્થિર સ્થિતિમાં આવતો હોય તો સ્થિર થયા પહેલાં બ્લોક કાપેલ અંતર ...... $m$ છે.View Solution
- 8$1 \,kg$ દળવાળા એક પથ્થરને એક દોરી સાથે બાંધેલ છે અને $1 \,m$ ત્રિજ્યાવાળા એક શિરોલંબ વર્તુળનાં ફેરવામાં આવે છે. જો ઉચ્ચત્તમ બિંદુએે તણાવ $14 \,N$ હોય તો ન્યૂનતમ બિંદુએ વેગ ........... $m / s$ હશે.View Solution
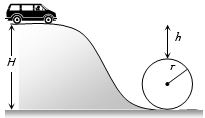
- 9View Solutionકાર એક પરિભ્રમણ પૂર્ણ કરતી હોય,તો...
- 10પાણીના પંપનો પાવર $2\;kW$ છે. જો $g = 10\,m/{\sec ^2}$ હોય, તો $1 \;min$ માં કેટલું પાણી ($liter$ માં) $10\; m$ ઊંચાઇ સુધી લઈ જઈ શકાય?View Solution
