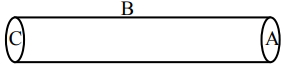
એક પોલા નળાકારમાં $q$ કુલંબ વિદ્યુતભાર રહેલો છે.જો નળાકારની વક્રાકાર સપાટી $B$ સાથે સંકળાયેલ ફલક્સ $\phi \;volt-meter$ હોય, તો સમતલ સપાટી $A$ સાથે સંકળાયેલ ફલક્સ $V-m$ એકમમાં કેટલું હશે?

AIPMT 2007,AIIMS 2008, Medium
d
Let \({\phi _A},{\phi _B}\) and \({\phi _C}\) are the electric flux linked with \(A,B\) and \(C.\)
Let \({\phi _A},{\phi _B}\) and \({\phi _C}\) are the electric flux linked with \(A,B\) and \(C.\)
According to gauss theorem,
\({\phi _A} + {\phi _B} + {\phi _C} = \frac{q}{{{\varepsilon _0}}}\)
\(\sin ce\,{\phi _A} = {\phi _C},\)
\(\therefore \,2{\phi _A} + {\phi _B} = \frac{q}{{{\varepsilon _0}}}\,\,\,or\,\,2{\phi _A} = \frac{q}{{{\varepsilon _0}}} - {\phi _B}\)
or, \(2{\phi _A} = \frac{q}{{{\varepsilon _0}}} - \phi \)
(Given \({\phi _B} = \phi \)).
\(\therefore {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\phi _A} = \frac{1}{2}\left( {\frac{q}{{{\varepsilon _0}}} - \phi } \right).\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિદ્યુતભાર $Q$ અને $-3Q$ અમુક અંતરે મૂકેલા છે,$Q$ પર વિદ્યુતક્ષેત્ર $E$ હોય,તો $-3Q$ પર વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
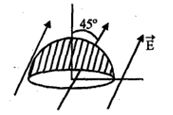
- 2સમક્ષિતિજ સમતલમાં તેની અંદરની બાજુની રેખા પર કોઈ વિદ્યુતભાર ન હોય તેવો $a$ ત્રિજ્યાનો સમતલ સપાટી વાળો એક અર્ધ ગોળો છે. તેની શિરોલંબ દિશા સાથે $\pi /4$ ખૂણો બનાવે તેમ સમાન વિદ્યુતક્ષેત્ર આવેલું છે. અર્ધ ગોળાની વક્ર સપાટીમાંથી પસાર થતું વિદ્યુત ફલક્સ ....... છે.View Solution
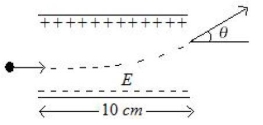
- 3બે સમાંતર પ્વેટ (તક્તિ)ની વચ્યે $10\,N/C$ નું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન થાય છે. એક ઇલેક્ટોન $0.5\,eV$ ગતિઊર્જા સાથે તક્તિઓની વચ્યેના વિસ્તારમાં સંમિતિ પૂર્વક દાખલ થાય છે. દરેક તક્તિઓની લંબાઈ $10\,cm$ છે. જ્યારે ઈલેકટ્રોન આ ક્ષેત્રના વિસ્તારમાંથી બહાર નીકળે ત્યારે તેના ગતિપથના વિચલન કોણ $(\theta)$ $...........^{\circ}$ (ડિગ્રી) થશે.View Solution
- 4એક વિદ્યુત દ્રીધ્રુવીને $2 \times 10^5\,N C ^{-1}$ તીવ્રતાના વિદ્યુતક્ષેત્ર સાથે $30^{\circ}$ ના ખૂણે મૂકેલી છે. તે $4\,N m$ જેટલું ટોર્ક અનુભવે છે.જો દ્રીધ્રુવીની લંબાઈ $2\,cm$ હોય તો દ્રીધ્રુવી પરના વીજભારની ગણતરી કરો.View Solution
- 5$L=20\, cm$ લંબાઈ ધરાવતા તારમાંથી અર્ધવર્તુળાકાર ચાપ બનાવવામાં આવે છે.જો ચાપના સમાન બે અડધા ભાગમાં એકસમાન રીતે $+Q$ અને $-Q$ $\left[ {\left| Q \right| = {{10}^3}{\varepsilon _0}} \right]$ કુલંબ વિજભાર પથરાયેલો છે.[જ્યાં $\varepsilon _0$ એ શૂન્યાવકાશની પરમિટિવિટી ($SI$એકમમાં)] અર્ધવર્તુળાકાર ચાપના કેન્દ્ર પાસે કુલ વિદ્યુતક્ષેત્ર કેટલું મળે?View Solution
- 6$-q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો એક કણ અનંત લંબાઈ અને $+\lambda$ જેટલી રેખીય વિદ્યુતભાર ધનતા ધરાવતા રેખીય વિદ્યુતભારને ફરતે $r$ ત્રિજ્યા ધરાવતા વર્તુળ ઉપર ગતિ કરે છે. આવર્તકાળ___________વડે આપી શકાય.View Solution
( $k$ ને કુલંબના અચળાંક તરીકે લો.)
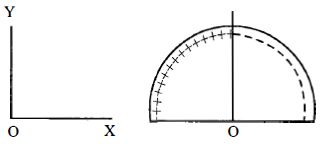
- 7કેન્દ્ર $O$ પર વિદ્યુતક્ષેત્ર કઈ દિશામાં હશે?View Solution

- 8View Solutionઇલેક્ટ્રીક ડાઈપોલને અસમાન વિધુતક્ષેત્રમાં મુક્તા તે .............. અનુભવે છે
- 9$R$ ત્રિજયાના ગોળીય કવચમાં કેન્દ્રથી અંતર નો વિદ્યુતક્ષેત્ર $E$ વિરુધ્ધનો આલેખ કેવો થાય?View Solution
- 10$2\,g$ દળ ધરાવતા લોલક પર $5.0\,\mu C$ વિજભાર છે.જેને એકસમાન $2000\,\frac{V}{m}$ જેટલા વિદ્યુતક્ષેત્રમાં મુકેલ છે સંતુલને લોલકે શિરોલંબ સાથે બનાવેલો ખૂણો કેટલો હશે?($g = 10\,\frac{m}{{{s^2}}}$)View Solution
