એક પોટેન્શિયોમીટર પરિપથમાં $1.5\, {V}$ નું $EMF$ ધરાવતા કોષ દ્વારા તારની $36\,{cm}$ અંતરે સમતોલન બિંદુ મળે છે.જો પ્રથમ કોષને બદલે $2.5\, {V}$નું $EMF$ ધરાવતો બીજો કોષ બદલવામાં આવે તો તારની કઈ લંબાઈએ સંતુલન બિંદુ મળશે? ($cm$માં)
NEET 2021, Medium
Download our app for free and get started
a
\(\phi=\) constant
\(\phi=\) constant
\(E_{\text {unknown }}=\phi I_{b} \Rightarrow E_{\text {unknown }} \propto I_{b}\)
\(\frac{E_{1}}{E_{2}}=\frac{I_{1}}{I_{2}} \Rightarrow \frac{1.5}{2.5}=\frac{36}{x}\)
\(x=\frac{36 \times 5}{3}=60\, \mathrm{~cm}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$196 \,\Omega - 1\,W$ મૂલ્ય ધરાવતા અવરોધના છેડાઓ પર કેટલો મોટો વોલ્ટેજ તમે સલામત રીતે મૂકી શકો ? .......... $volt$View Solution
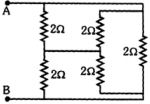
- 2$AB$ ના છેડા વચ્ચેનો સમતુલ્ય અવરોધ............. $\Omega$ છે.View Solution
- 3તારમાં વિધુત પ્રવાહ સમય પર $i = (2 + 3t)A$. પ્રમાણે આધાર રાખે છે $10$ સેકન્ડમાં તારના આડછેદમાંથી પસાર થયેલા વિધુતભારની ગણતરી ............... $C$ કરો.View Solution
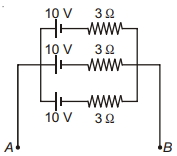
- 4$AB$ની વચ્ચે ત્રણ એકસમાન કોષોને સમાંતરમાં જોંડેલ છે. $A B$ની વચ્ચે કુલ $emf$ $..........V$ છે.View Solution
- 5જુદાં જુદાં દ્રવ્યમાંથી બનાવેલ અવરોધના $0\,^\circ$$C$ તાપમાને મૂલ્ય $R_1$ અને $R_2$ છે.તેમના અવરોધના તાપમાન ગુણાંક $\alpha $ અને $ - \beta $ છે.જો શ્રેણીમાં જોડવાથી તાપમાન સાથે સમતુલ્ય અવરોધ બદલાતો ન હોય,તો ${R_1}/{R_2}=$View Solution
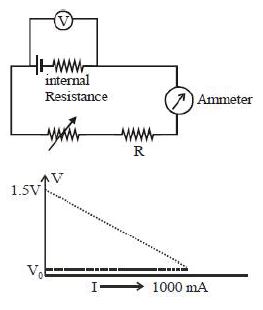
- 6ઓહમના નિયમને સાબિત કરવા એક વિદ્યાર્થી આકૃતિમાં દર્શાવ્યા પ્રમાણે બેટરી સાથે વોલ્ટમીટર જોડે છે.તેના માટે વૉલ્ટ વિરુદ્ધ પ્રવાહનો આલેખ દર્શાવેલ છે.જો $V_0$ લગભગ શૂન્ય જેટલો હોય તો નીચેનામાથી કયું વિધાન સાચું હશે?View Solution
- 7$R$ અવરોધ ધરાવતા,એક સમાન તારને $V _0$ જેટલો સ્થિતિમાન લગાડવામાં આવે છે. આ દરમ્યાન વિખેરીત થતો પાવર $P_1$ છે. ત્યારબાદ તારને બે ભાગમાં કાપવામાં આવે છે અને આ દરેક અડધા ભાગને $V_0$ જેટલો વોલ્ટેજ લગાડવામાં આવે છે. બીજા કિસ્સા માં વિખેરીત થતો પાવર $P _2$ વિખેરીત થતા પાવરનો ગુણોત્તર $P _2$ અને $P _1$ નું મૂલ્ય $\sqrt{x}: 1$ છે. $x$ નું મૂલ્ય ........ છે.View Solution
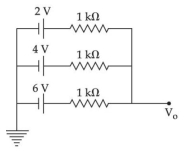
- 8આપેલ આકૃતિમાં, $V_0$ ની કિંમત $.........V$ હશે.View Solution
- 9એક પોટેન્શિયોમીટરના પ્રયોગમાં કોષ માટે બેલેન્સિંગ લંબાઈ $560 \;\mathrm{cm}$ છે હવે જો $10 \;\Omega$ ના અવરોધને કોષ સાથે સમાંતરમાં જોડતા બેલેન્સિંગ લંબાઈ $60\; \mathrm{cm} $ મળે છે.જો કોષનો આંતરિક અવરોધ $\frac{\mathrm{N}}{10} \;\Omega,$ હોય તો $\mathrm{N}$ નું મૂલ્ય કેટલું હશે?View Solution
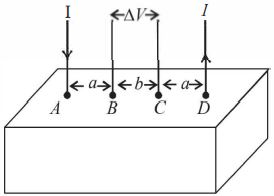
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણેનાં $\rho $ અવરોધકતાનાં વાહક દ્રવ્યને એક ચોસલો ધારો. વિદ્યુત પ્રવાહ $I, A$ આગળ દાખલ થાય છે $D$ આગળથી છોડે (બહાર નીકળે) છે. $B$ અને $C$ વચ્ચે ઉદભવતાં વોલ્ટેજ $\Delta V$ શોધવા સંપાતપણા સિદ્ધાંત લાગુ પાડવામાં આવે છે. નીચેના ક્રમમાં ગગણતરી કરવામાં આવે છે.View Solution
$[A]$ $A$ માંથી દાખલ થતો વિદ્યુત પ્રવાહ $I$ લો અને ચોસલામાં તે એક અર્ધ ગોળાકાર સપાટી ઉપર પ્રસરે છે. તેમ માનવામાં આવે.
$[B]$ઓહમનો નિયમ $E = \rho j $ ને ઉપયાગ કરીને $A$ થી $r$ અંતરે વિદ્યુત ક્ષેત્ર $E (r)$ ગણવામાં આવે જ્યાં $j,r$ આગળ દર એકમ ક્ષેત્રફળે વિદ્યુત પ્રવાહ છે.
$[C]$ $E (r)$ નાં $r$ પરનાં આધારપણા પરથી $r$ આગળ સ્થિતિમાન $V (r)$ મેળવવામાં આવે.
$[D]$$D$ માંથી મહાર નીકળતા ($D$ ને છોડતા) વિદ્યુત પ્રવાહ $ I$ માટે $(i)$ અથવા
$A$ આગળ દાખલ થતાં વિદ્યુત પ્રવાહ માટે $A$ થી $r$ અંતરે વિદ્યુત ક્ષેત્ર ........... થાય.
